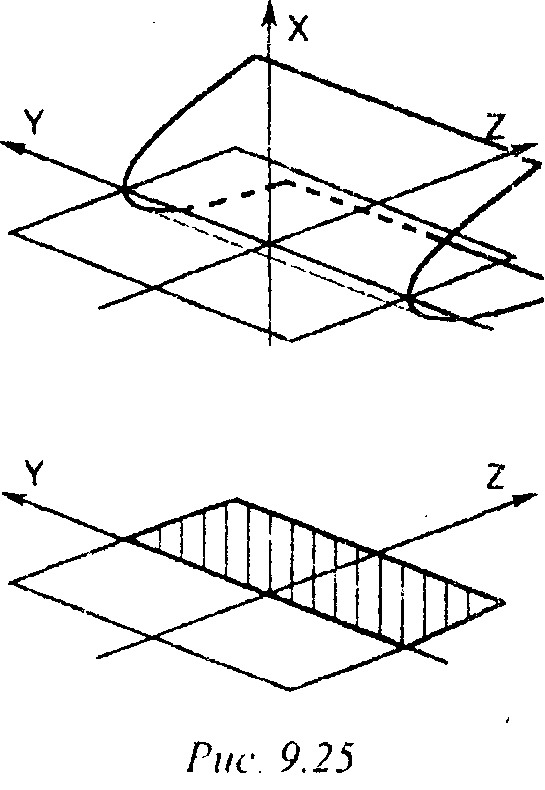
V )Здесь, в отличие от первого случая, точки плоскости А = 0 разбиваются на три класса:
к первому относятся точки (2 > 0), у которых два прообраза (рис. 9.25 этот класс заштрихован);
ко второму - те, у которых прообраз один (2=0);
и наконец, к третьему классу относятся точки, у которых прообразов на цилиндре нет вовсе.
Прямая X = 0, 2 - 0 является особой.
-» ->Вдоль нее векторы N и Т ортогональны.
Особенность этого типа называется складкой.
Компьютерная графика. Полигональные модели
3-й случай. Рассмотрим поверхность, заданную уравнением 2 = Х3 + ХУ-2 = 0.
Вычислим нормальный вектор этой поверхности
/? = (зх2 + у,х,-\)
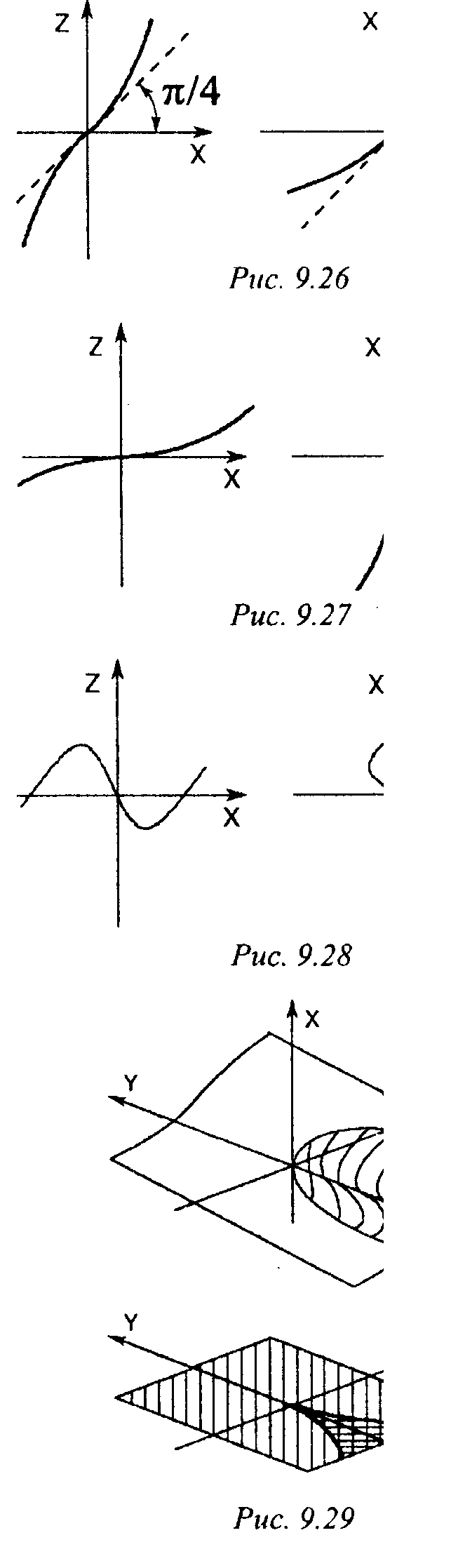
и построим ее, применив метод сечений/ Пусть У = 1. Тогдаг = Х3+Х
(рис. 9.26).
При 7= 0 имеем 2-Х? (рис. 9.27).
Наконец, при У = -1 получаем Ъ = X3 - X (рис. 9.28).
Построенные сечения дают представление обо всей поверхности. Поэтому нарисовать ее теперь уже несложно (рис. 9.29).
Из условия
_^ _^(Ы9Ь) = ЗХ2 +У = 0
*и уравнения поверхности получаем, что вдоль лежащей на ней кривой с уравнениями У - -ЗХ2,2 = -2Х3
->вектор проектирования Ь и нормаль-
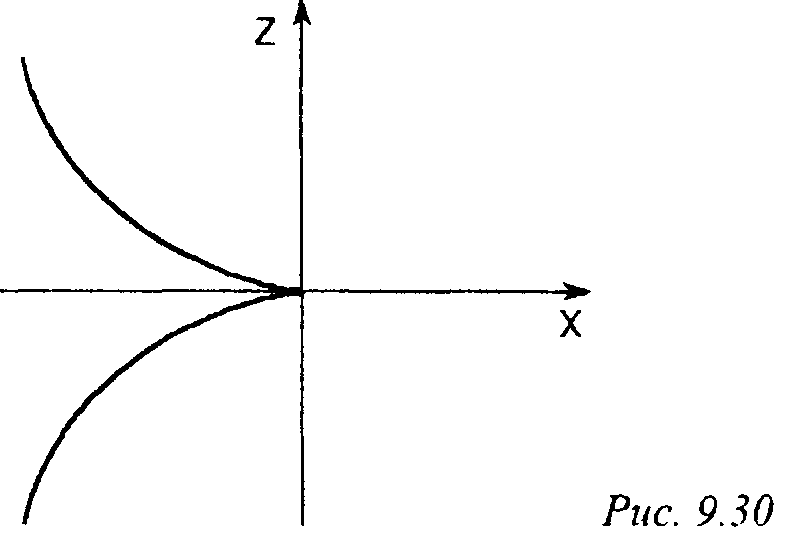
-»ный вектор N рассматриваемой поверхности ортогональны. Исключая X, получаем,что
(-у/з)3 =(-г/2)2, или 2722 =-4У3.
Последнее равенство задает на координатной плоскости X - 0 полукубическую
9. Преобразования в пространстве, проектирование параболу (рис. 9.30), которая делит точки этой плоскости на три класса: к первому относятся точки, лежащие на острие (у каждой из них на заданной поверхности ровно два прообраза), внутри острия лежат точки второго класса (каждая точка имеет по три прообраза), а вне - точки третьего класса, имеющие по одному прообразу. Особенность этого типа называется сборкой.
Замечание. Возникающая в третьем случае полукубическая парабола имеет точку заострения. Однако ее прообраз Х=ХУУ=-ЪХ2,1 = -2ХЪ
является регулярной кривой, лежащей на заданной поверхности.
В теории особенностей (теории катастроф) доказывается: при проектировании на плоскость произвольного гладкого объекта - поверхности возможны (с точностью до малого шевеления, рассыпающего более сложные проекции) только три указанных типа проекции - обыкновенная проекция, складка и сборка.
