Компьютерная графика. Полигональные модели
res.x [0][2] = axis.x*axis.z*(1-cosine)+axis.y*sine; res.x [1][2] = axis.y*axis.z*(1-cosine)-axis.x*sine; res.x [2][2] = axis.z*axis.z+(1-axis.z*axis.z)*cosine; res.x [3][2] = 0;
res.x (0][3] = 0; res.x [1)[3] = 0; res.x [2][3] = 0; res.x [3][3] = 1;
return res;
}
Matrix mirrorX {)
{
.» Matrix res ( 1 ); res.x [0][0] = -1; return res;
}
Matrix mirrorY ()
{
Matrix res (1 ); res.x (1][1] = -1; . return res;
}
Matrix mirrorZ ()
{
Matrix res (1 ); res.x [2][2] = -1 ; return res;
}9.3. Особенности проекций гладких отображений В заключение этой главы мы остановимся на некоторых эффектах, возникающих при проектирований искривленных объектов (главным образом поверхностей) на картинную плоскость.
Важно отмегить, что описываемые ниже эффекты возникают вне зависимости от того, является ли проектирование параллельным или центральным.
Будем считать для простоты, что проектирование проводится при помощи пучка параллельных прямых, идущих перпендикулярно картинной плоскости, а система координат X, У, Z в пространстве выбрана так, что картинная плоскость совпадает с координатной плоскостью X = 0.
Укажем три принципиально различных случая.
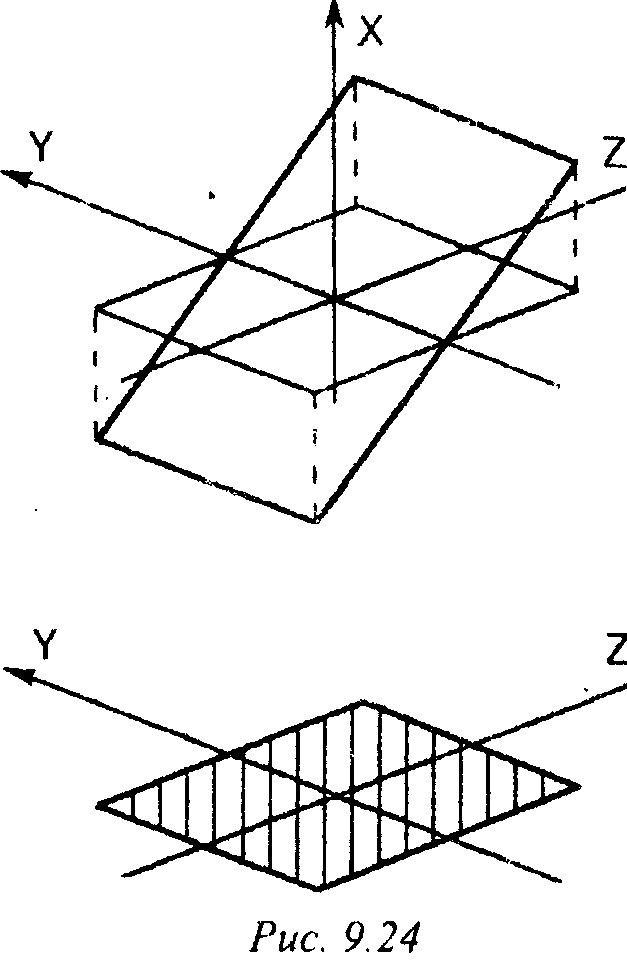
1-й случай. Заданная поверхность - плоскость, описываемая уравнением Z = X и проектируемая на плоскость X = 0 (рис. 9.24).
9. Преобразования в пространстве, проектирование Записав ее уравнение в неявном виде X - 7.-0, вычислим координаты нормального вектора. Имеем
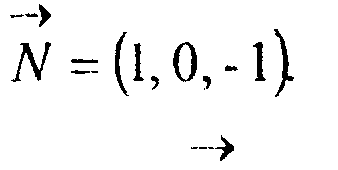
Вектор ь , вдоль которого осуществляется проектирование, имеет координаты _^
I = (1, о, о)
Легко видеть, что скалярное произведение этих двух векторов отлично от нуля:
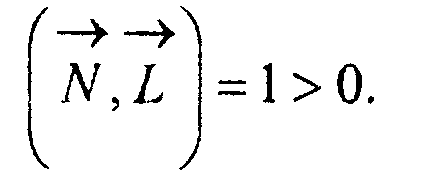
Тем самым вектор проектирования и нормальный вектор рассматриваемой поверхности не перпендикулярны ни в одной точке.
Отметим, что полученная проекция особенностей не имеет.
2-й случай. Заданная поверхность - параболический цилиндр с уравнением 2 ~ Х\\\тХ2 -2 = 0.
-> -» Нормальный вектор N = (2Х, О, -1) ортогонален вектору проектирования Ь
в точках оси У. Это вытекает из того, что
