При триметрии длины проекций попарно различны.

Проекции, для получения которых используется пучок прямых, не перпендикулярных плоскости экрана, принято называть косоугольными.

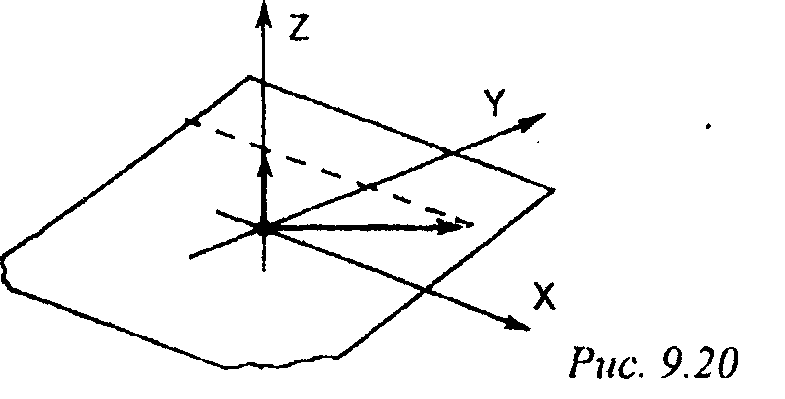
При косоугольном проектировании орта оси 2 на плоскость ЛТ(рис. 9.20) имеем:

(0 0 1 1)->(а Р 0 1).

Матрица соответствующего преобразования имеет следующий вид:

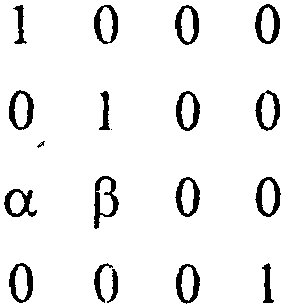
Выделяют два вида косоугольных проекций: свободную проекцию (угол наклона проектирующих прямых к плоскости экрана равен половине прямого) и кабинетную проекцию (частный случай свободной проекции - масштаб по третьей оси вдвое меньше).

к В случае свободной проекции а = р = cos -, п 1 К

в случае кабинетной - а = р = - cos -.

2 4

Перспективные (центральные) проекции строятся более сложно.

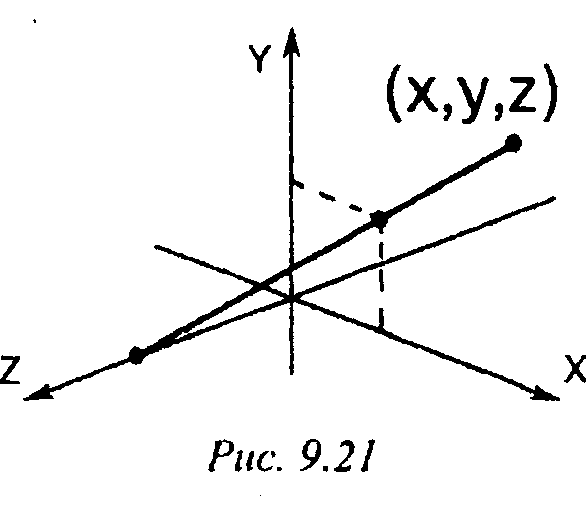
Предположим для простоты, что центр проектирования лежит на оси Z в точке С(0, 0, с) и плоскость проектирования совпадает с координатной плоскостью XY (рис. 9.21). Возьмем в пространстве * произвольную точку М(х, у, z), проведем через нее и точку С прямую и запишем соответствующие параметрические уравнения.

Имеем:

X* =xt,Y* =yt,Z* = c + (z--c)t.

Найдем координаты точки пересечения построенной прямой с плоскостью ЛТ. Из условия Z* = 0 получаем, что

9. Преобразования в пространстве, проектирование

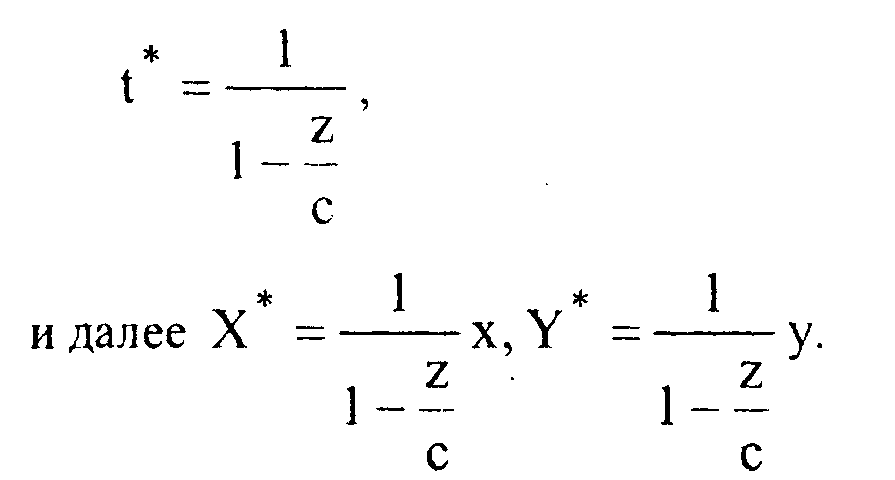
Интересно заметить, что тот же самый результат можно получить, привлекая матрицу

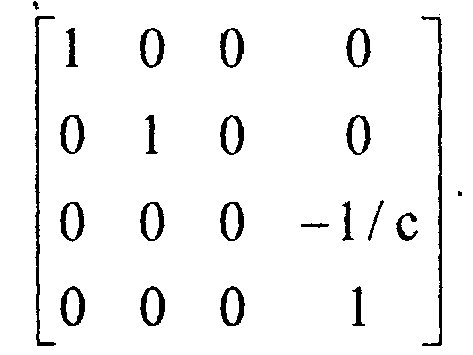
I

В самом деле, переходя к однородным координатам, прямым вычислением совсем легко проверить, что

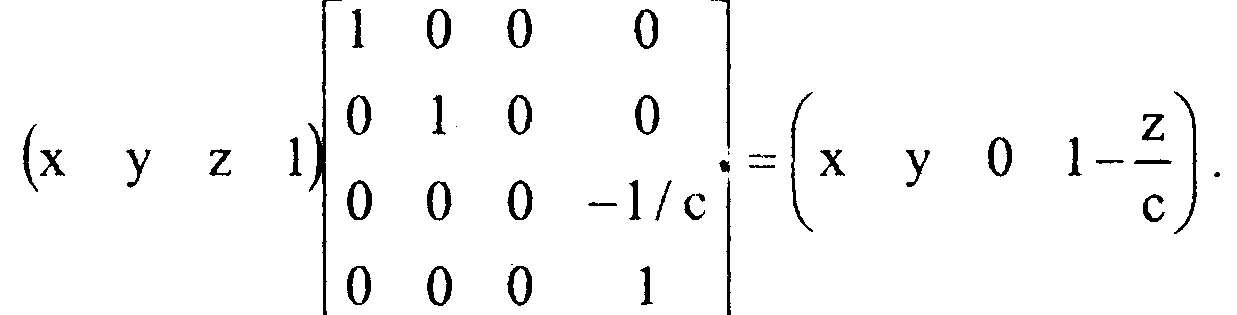
Вспоминая свойства однородных координат, запишем полученный результат в несколько ином виде: и затем путем непосредственного сравнения убедимся в том, что это координаты той же самой точки.

Замечание. Матрица проектирования, разумеется, вырожоенна.

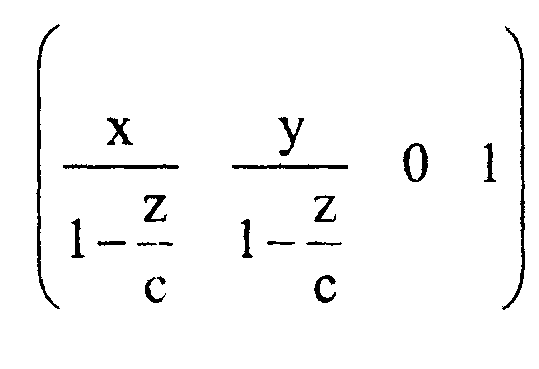
Матрица соответствующего перспективного преобразования (без проектирования) имеет следующий вид: Обратим внимание на то, что последняя матрица невырожденна.

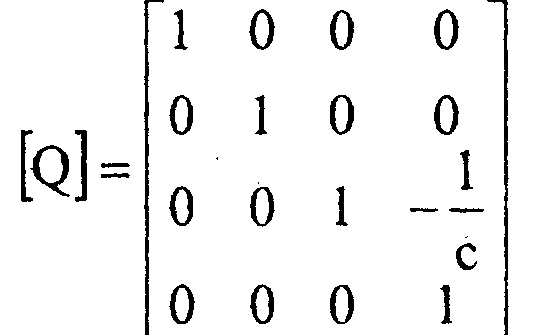
Рассмотрим пучок прямых, параллельных оси 2, и попробуем разобраться в том, что с ним происходит под действием матрицы [0\.

Каждая прямая пучка однозначно определяется точкой (скажем, М(х, у, г)) своего пересечения с плоскостью АТ и описывается уравнениями X = х, У = у, 2 = I.

⇐ Предыдущая| |Следующая ⇒