Схема I

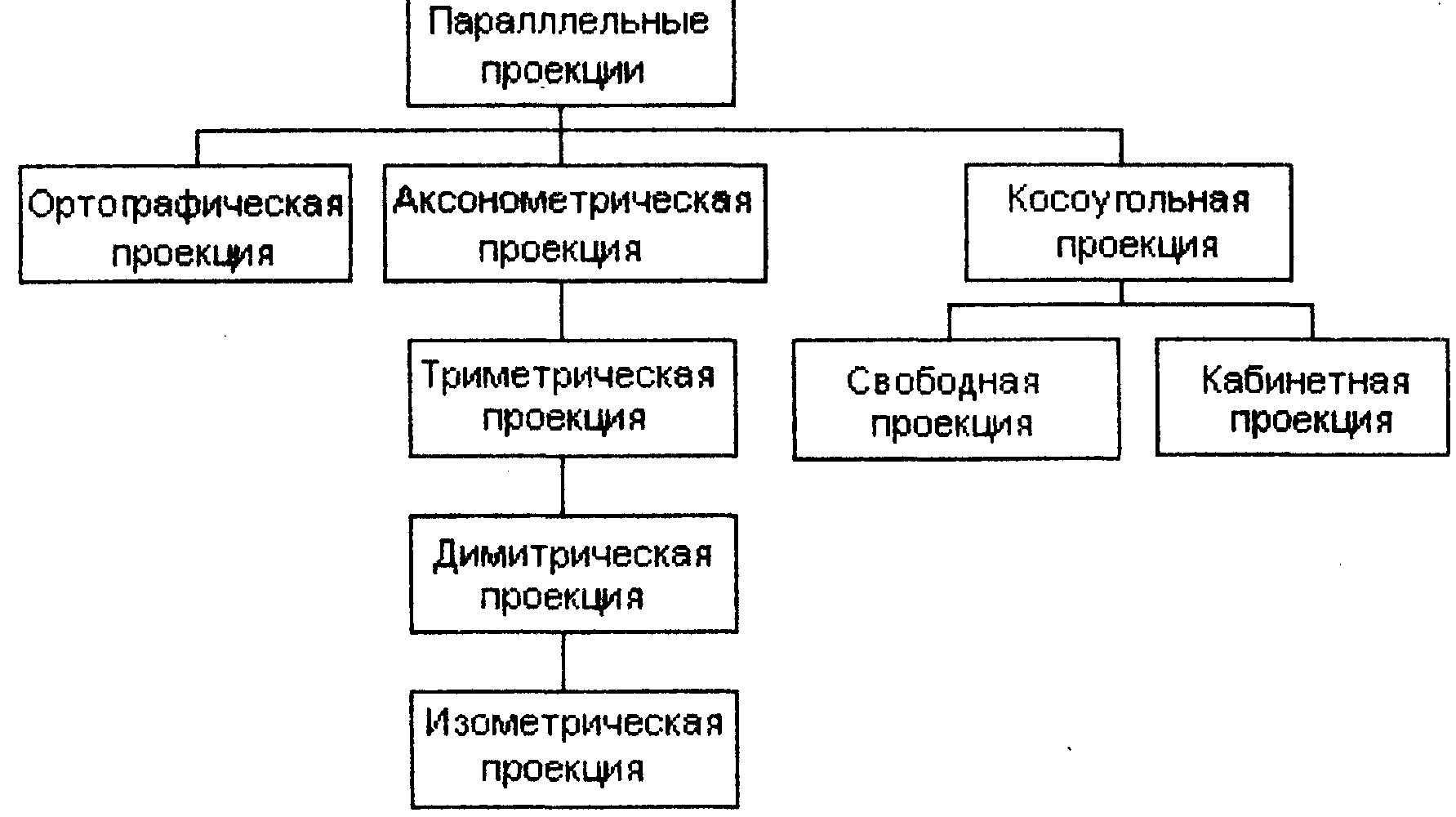
Компьютерная графика. Полигональные модели

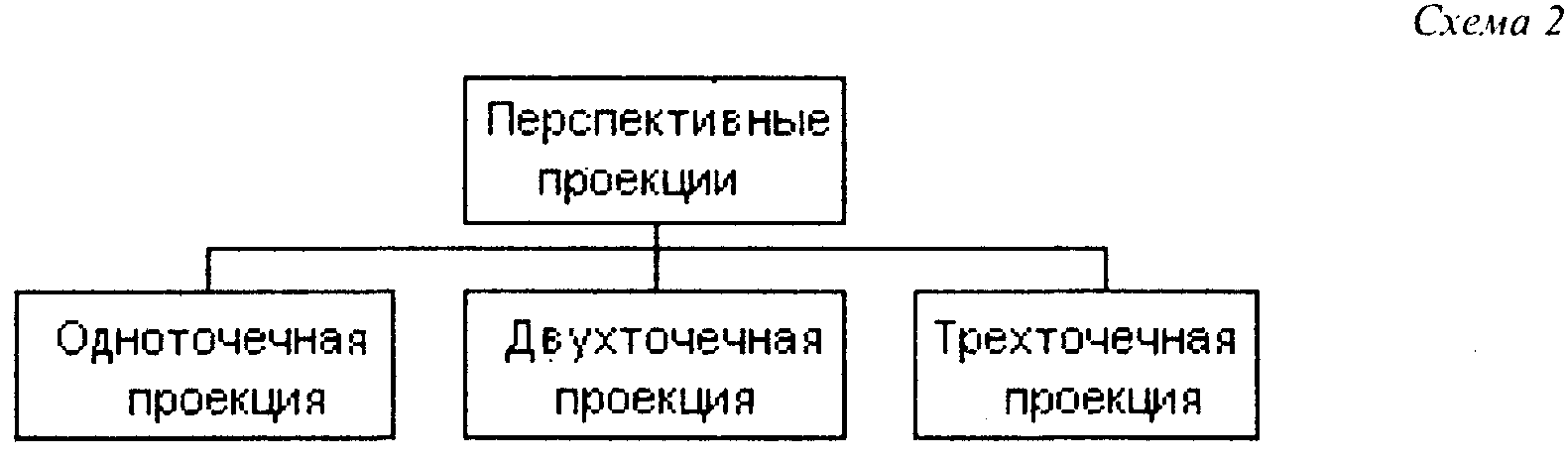
Важное замечание. Использование для описания преобразований проектирования однородных координат и матриц четвертого порядка позволяет упростить изложение и зримо облегчает решение задач геометрического моделирования.

При ортографической проекции картинная плоскость совпадает с одной из координатных плоскостей или параллельна ей (рис. 9.16). Матрица проектирования вдоль оси Хна плоскость У7 имеет вид:

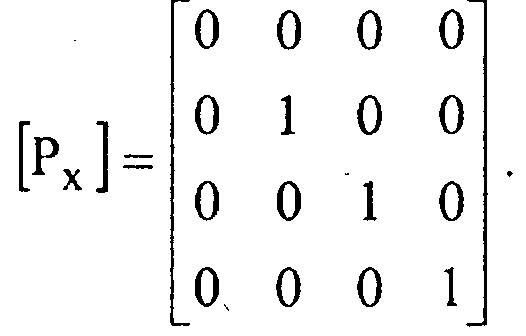
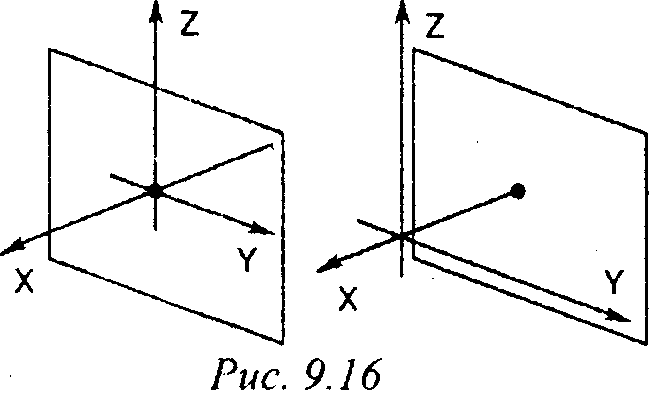
В случае, если плоскость проектирования параллельна координатной плоскости, необходимо умножить матрицу [7\] на матрицу сдвига. В результате получаем Аналогично записываются матрицы проектирования вдоль двух других координатных осей:

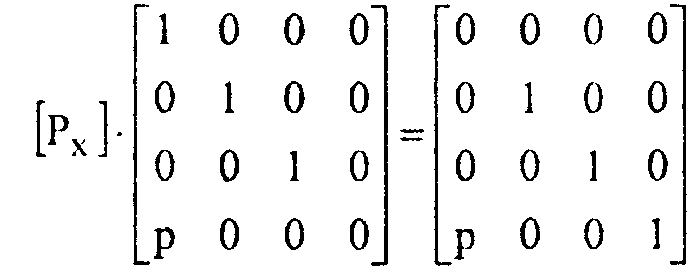
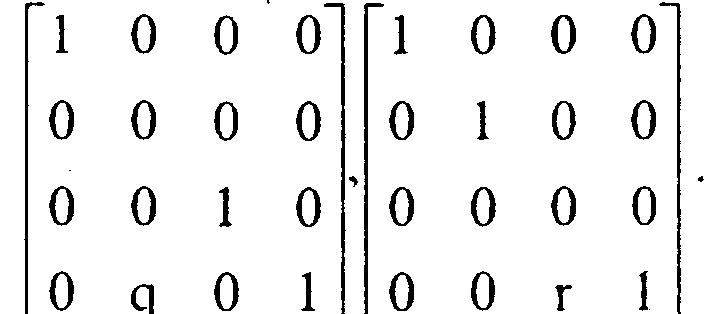
Замечание. Все три полученные матрицы проектирования вырождении.

При аксонометрической проекции проектирующие прямые перпендикулярны картинной плоскости.

В соответствии со взаимным расположением плоскости проектирования и координатных осей различают три вида проекций:

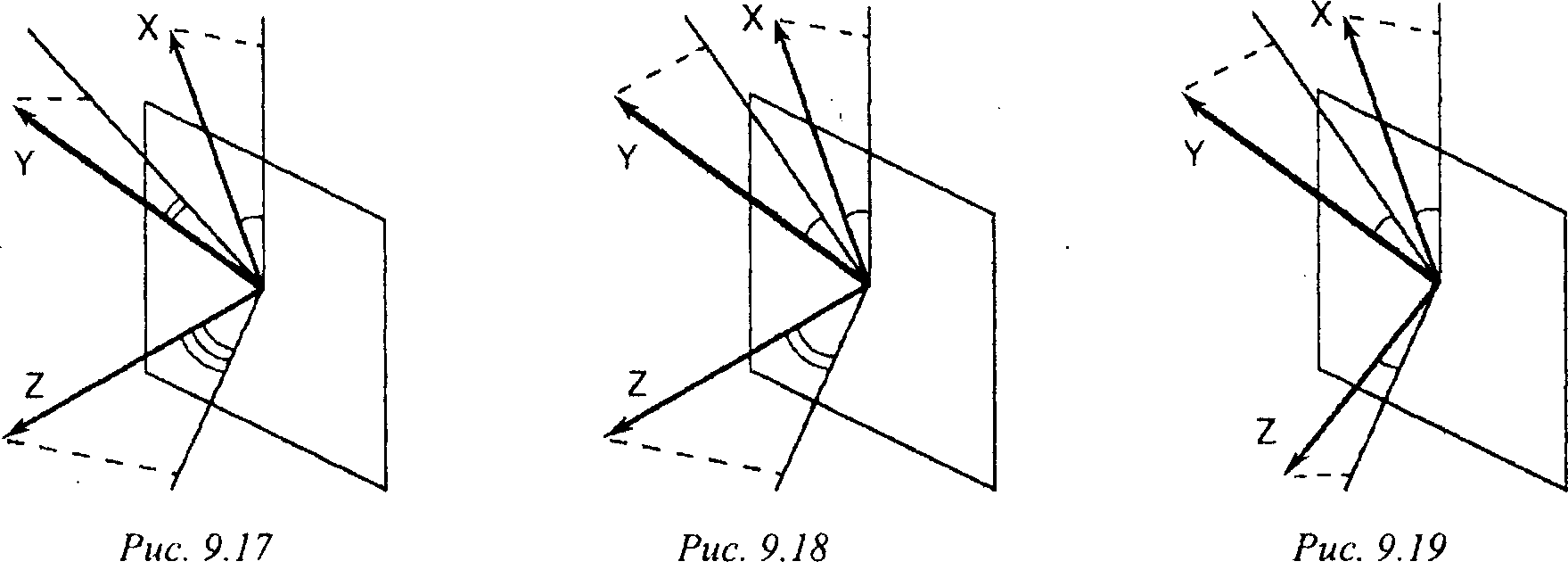
триметрию - нормальным вектор картинной плоскости образует с ортами координатных осей попарно различные углы (рис. 9.1 7);

9. Преобразования в пространстве, проектирование

диметрию - два угла между нормалью картинной плоскости и координатными осями равны (рис. 9.18);

изометрию - все три угла между нормалью картинной плоскости и координатными осями равны (рис. 9.19).

Каждый из трех видов указанных проекций получается комбинацией поворотов, за которой следует параллельное проектирование. При повороте на угол у/ относительно оси ординат, на угол ср вокруг оси абсцисс и последующего проектирования вдоль оси аппликат возникает матрица

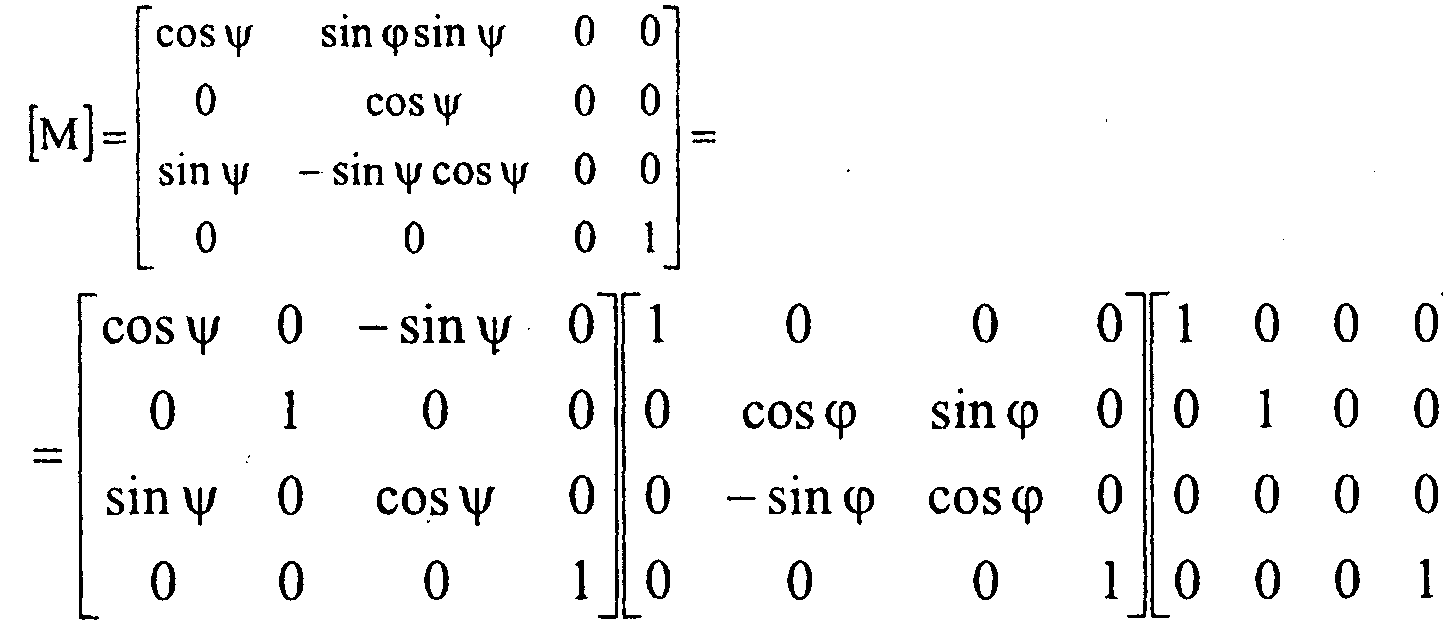
Покажем, как при этом преобразуются единичные орты координатных осей Z, У, Z; (l 0 0 l)[M] = (cosy sincpsiny 0 l),

(О 1 0 l)[M] = (0 coscp 0 \\

(О 0 1 l)[M] = (siny - sin ф cos у 0 l)

Диметрия характеризуется тем, что длины двух проекций совпадают:

2 2 2 2

cos y+sdn ф sin у = COS ф.

Отсюда следует, что

2 2

sin у = tan ф.

В случае изометрии имеем Компьютерная графика. Полигональные модели

⇐ Предыдущая| |Следующая ⇒