Переходя к однородным координатам и используя матрицу [£>]. получаем Компьютерная графика. Полигональные модели
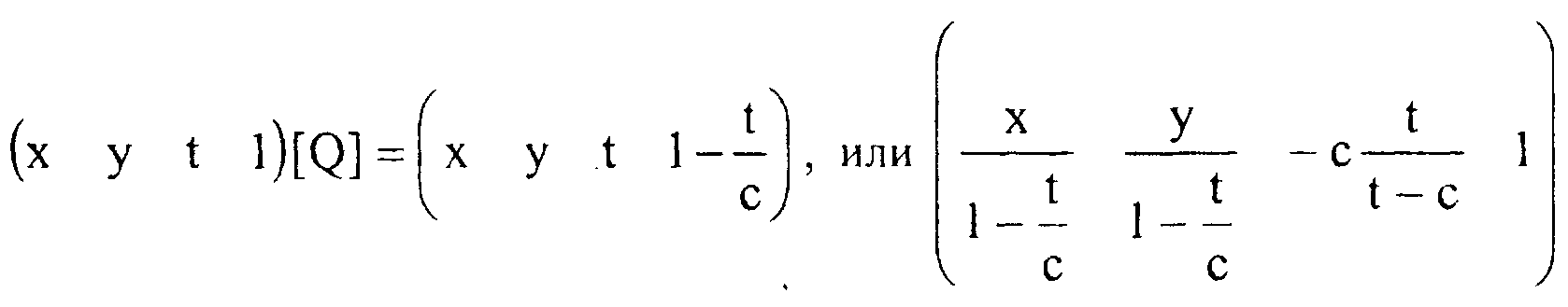
Устремим / в бесконечность.
При переходе к пределу точка (х, у, 1, 1) преобразуется в (0, 0, 1, 0). Чтобы убедиться в этом, достаточно разделить каждую координату на V.

рассматриваемого равенства.
Тем самым бесконечно удаленный (несобственный) центр (0, 0, 1,0) пучка прямых, параллельных оси 2, переходит в точку (0, 0, -с, 1) оси 2.
Вообще каждый несобственный пучок прямых (совокупность прямых, параллельных заданному направлению), не параллельный картинной плоскости,
X = х + и, у = у + тХ, 2 = г + ш, п ф 0, под действием преобразования, задаваемого матрицей [£?], переходит в собственный пучок
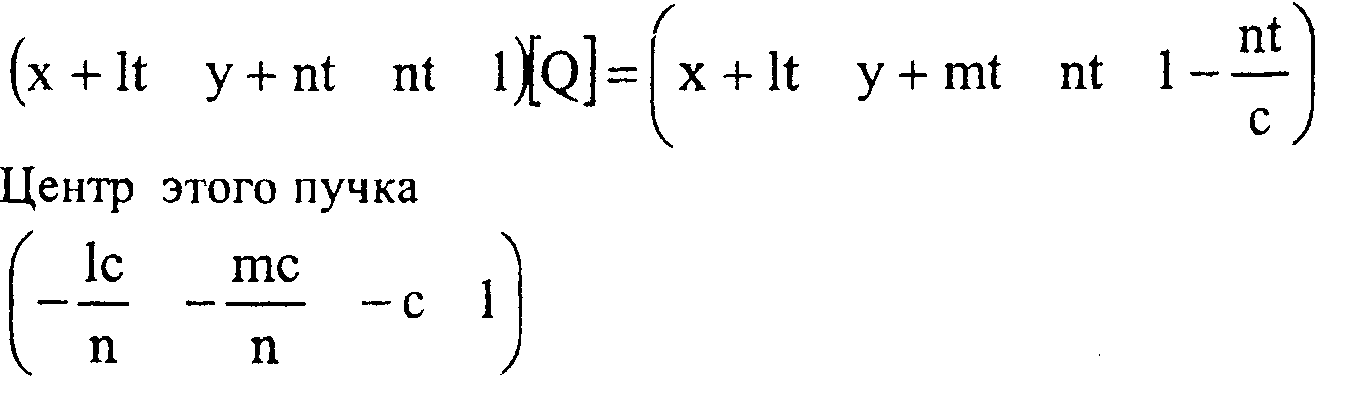
называют точкой схода.
Принято выделять так называемые главные точки схода, которые соответствуют пучкам прямых, параллельных координатным осям.
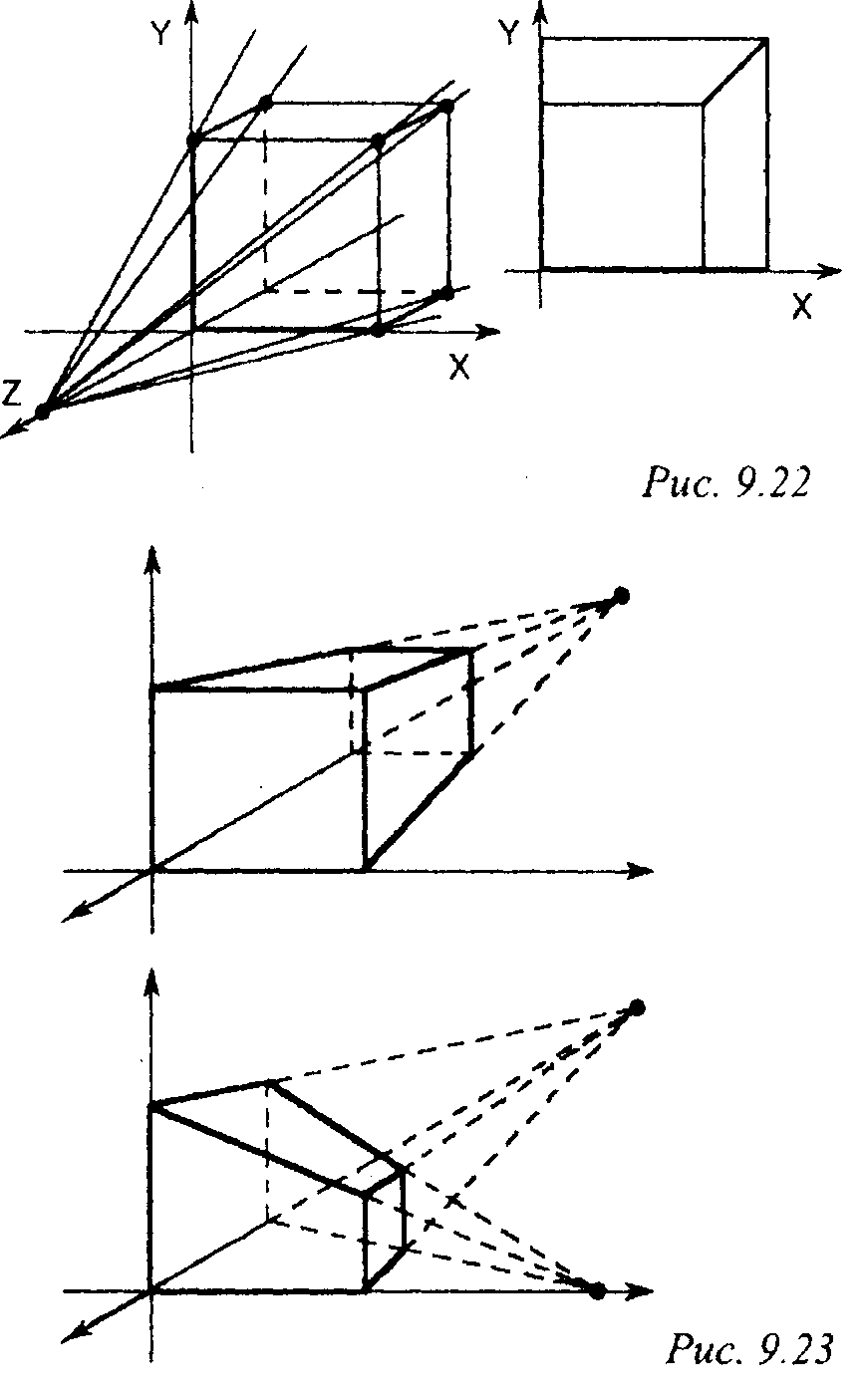
9. Преобразования в пространстве, проектирование Для преобразования с матрицей [()] существует лишь одна главная точка схода (рис. 9.22). В общем случае (когда оси координатной системы не параллельны плоскости экрана) таких точек три.
Матрица соответствующего преобразования выглядит следующим образом:
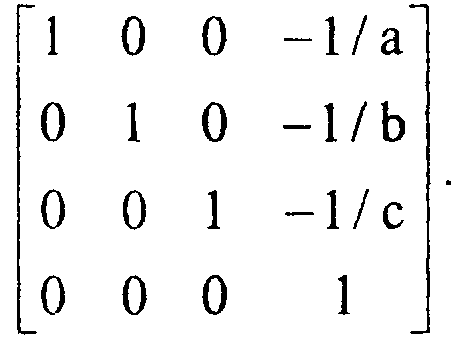
Пучок прямых, параллельных оси ОХ ОУ (10 0 0) (0 10 0)
переходит в пучок прямых с центром.
На рис. 9.23 изображены проекции куба со сторонами, параллельными координатным осям, с одной и с двумя главными точками схода
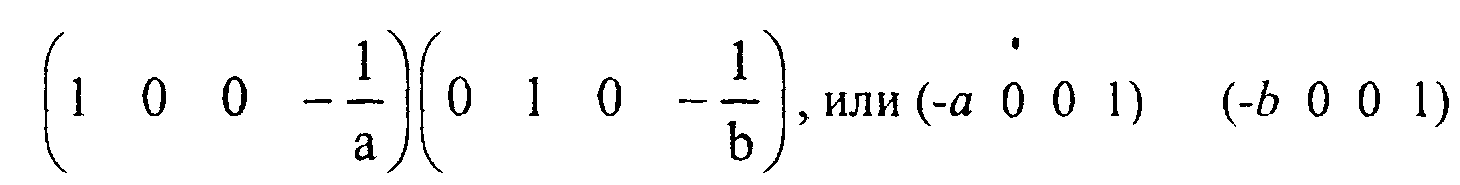
Точки (-а, О, 0) и (О, 0) суть главные точки схода.
По аналогии с двумерными объектами здесь также вводятся классы для работы с трехмерными векторами и матрицами преобразований. При этом поскольку в ряде случаев перспективное проектирование проводится отдельно и использование матриц 4x4 снижает общее быстродействие, то здесь вводится класс Vector3D для представления трехмерных векторов и два класса для работы с матрицами - класс Matrix3D, реализующий основные аффинные операции над векторами без использования однородных координат, и класс Matrix, служащий для работы с однородными координатами. Вводятся функции, возвращающие матрицы для ряда стандартных преобразований в пространстве.
