Декартовы координаты вершин построенного икосаэдра легко вычисляются. Для двух вершин они уже найдены, а что касается остальных 10 вершин икосаэдра, то достаточно заметить, что полярные углы соседних вершин треугольного пояса разнятся на 36°, а их полярные радиусы равны единице.
Остается построить додекаэдр.
https://premierpoker.online/s-vyvodom-pr/.
Оставляя в стороне способ, предложенный Евклидом (построение "крыш" над гранями куба), вновь воспользуемся свойством двойственности, но теперь уже связывающим додекаэдр и икосаэдр: вершины додекаэдра суть центры (тяжести) треугольных граней икосаэдра.
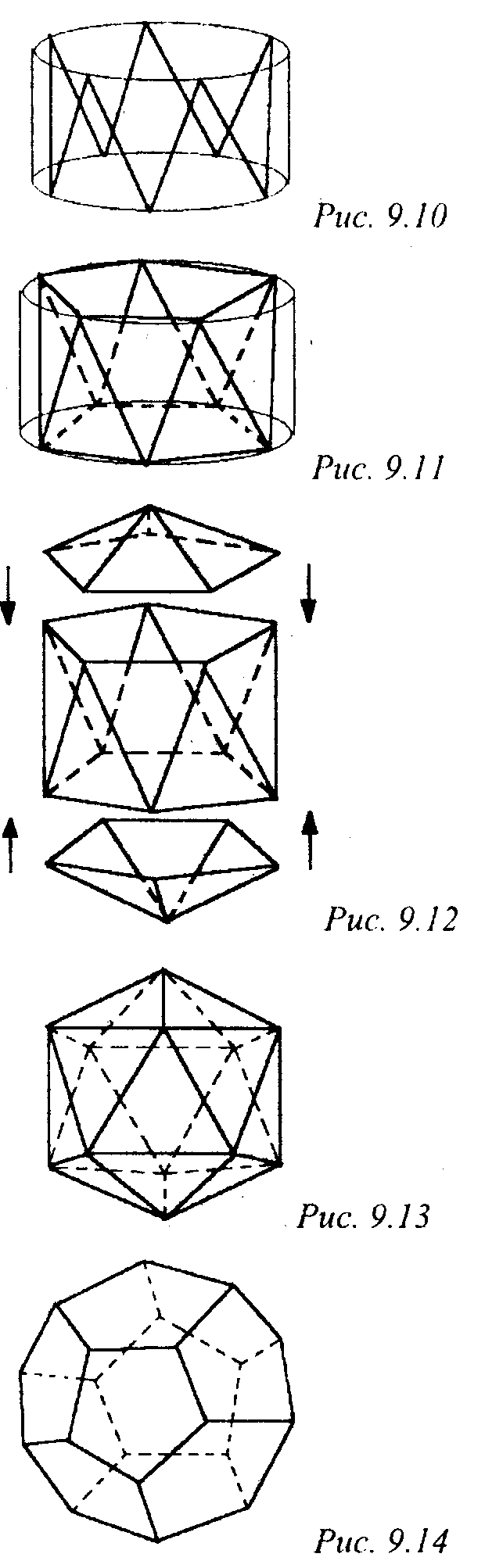
И значит, координаты каждой вершины додекаэдра можно найти, вычислив средние арифметические соответствующих координат вершин содержащей ее грани икосаэдра (рис. 9.14).
Замечание. Подвергая полученные правильные многогранники преобразованиям вращения и переноса, можно получить Платоновы тела с центрами в произвольных точках и с любыми длинами ребер.
В качестве упражнения полезно написать по предложенным способам программы, генерирующие все Платоновы тела.
9.2. Виды проектирования Изображение объектов па картинной плоскости связано с еще одной геометрической операцией - проектированием при помощи пучка прямых. В компьютерной
9. Преобразования в пространстве, проектирование графике используется несколько различных видов проектирования (иногда„называемого также проецированием). Наиболее употребимые на практике виды проектирования суть параллельное и центральное.
Для получения проекции объекта на картинную плоскость необходимо провести через каждую его точку прямую из заданного проектирующего пучка (собственного или несобственного) и затем найти координаты точки пересечения этой прямой с плоскостью изображения. В случае центрального проектирования все прямые исходят из одной точки - центра собственного пучка. При параллельном проектировании центр (несобственного) пучка считается лежащим в бесконечности (рис. 9 Л 5).
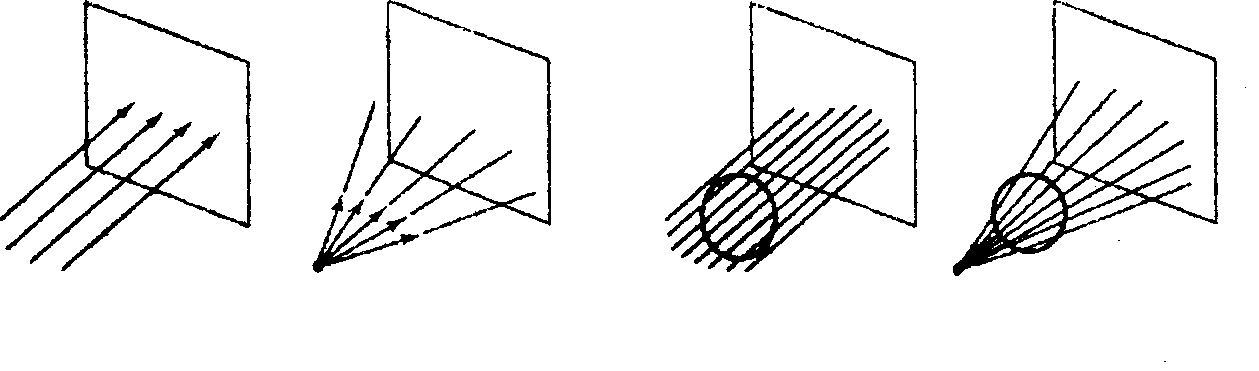
Рис. 9.15
Каждый из этих двух основных классов разбивается на несколько подклассов в зависимости от взаимного расположения картинной плоскости и координатных осей. Некоторое представление о видах проектирования могут дать приводимые ниже схемы.
