Покажем, как, используя куб, можно построить тетраэдр и октаэдр.
Для построения тетраэдра достаточно*провести скрещивающиеся диагонали противоположных граней куба (рис. 9.5).
Тем самым вершинами тетраэдра являются любые 4 вершины куба, попарно не смежные ни с одним из его ребер.
Для построения октаэдра воспользуемся следующим свойством двойственности: вершины октаэдра суть центры (тяжести) граней куба (рис. 9.6).
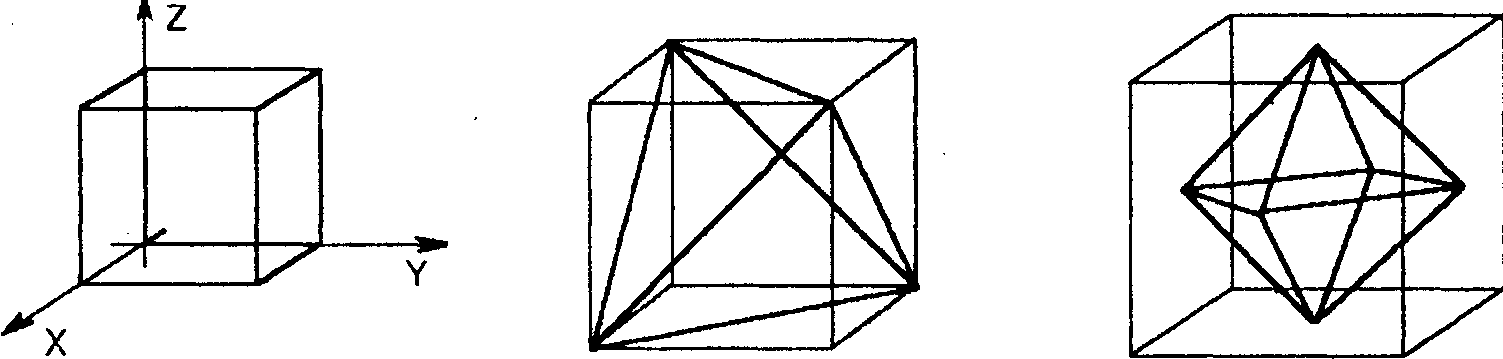
Рис. 9.4 Рис. 9.5 Рис. 9.6
И значит, координаты вершин октаэдра по координатам вершин куба легко вычисляются (каждая координата вершины октаэдра является средним арифметическим одноименных координат четырех вершин содержащей ее грани куба).
Додекаэдр и икосаэдр также можно построить при помощи куба. Однако существует, на наш взгляд, более простой способ их конструирования, который мы и собираемся описать здесь.
Начнем с икосаэдра.
Рассечем круглый цилиндр единичного радиуса, ось которого совпадает с осью аппликат Z двумя плоскостями Ъ - -0,5 и Ъ = 0,5 (рис. 9.7). Разобьем каждую из полученных окружностей на 5 равных частей так, как показано на рис. 9.8. Перемещаясь вдоль обеих окружностей против часовой стрелки, занумеруем выделенные 10 точек в порядке возрастания угла поворота (рис. 9.9) и затем последовательно, в соответствии с нумерацией, соединим эти точки прямолинейными отрезками (рис. 9.10).
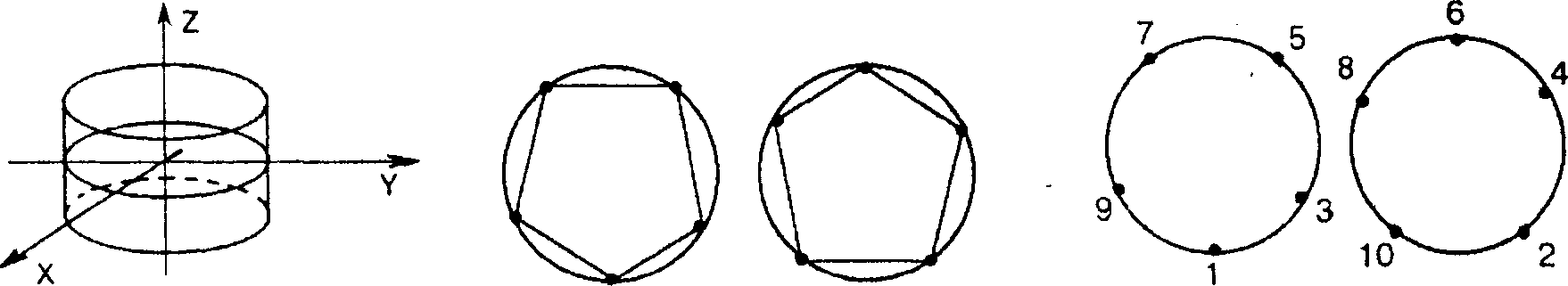
Рис. 9.7 Рис. 9.8 Рис. 9.9
Стягивая теперь хордами точки, выделенные на каждой из окружностей, мы получим в результате пояс из 10 правильных треугольников (рис. 9.11).
Компьютерная графика. Полигональные модели с аппликатами ± Для завершения построения икосаэдра выберем на оси 2 две точки так, чтобы длины боковых ребер пятиугольных пирамид с вершинами в этих точках и основаниями, совпадающими с построенными пятиугольниками (рис. 9.12), были равны длинам сторон пояса из треугольников.
Нетрудно видеть, что для этого годятся точки
1±В результате описанных построений получаем 12 точек. Выпуклый многогранник с вершинами в этих точках будет иметь 20 граней, каждая из которых является правильным треугольником, и все его многогранные углы при вершинах будут равны между собой. Тем самым результат описанного построения - икосаэдр (рис. 9.13).
