где Т]-- .
Тогда г)2 sin2 0j = sin2 0t
или
?i2(l-co^)=l-co^0t. Так как
cos 0| = (-i,n), cos0t = (-t,n),то a2(i,n)2 + 2aP(i,n) + p2 - 1 + r|2((i,n)2 -1). (2.3) Из условия нормировки вектора / имеем:
|t||2 = (t, t) = a2 + 2aP(i, n) + P2 = 1 . Вычитая это соотношение из равенства (2.3), получим a2((i,n)2 -l) = ti2((i,n)2 -1), откуда a = ±r\.
Компьютерная графика. Полигональные модели Из физических соображений ясно, что а = г|. Второй параметр определяется из уравнения
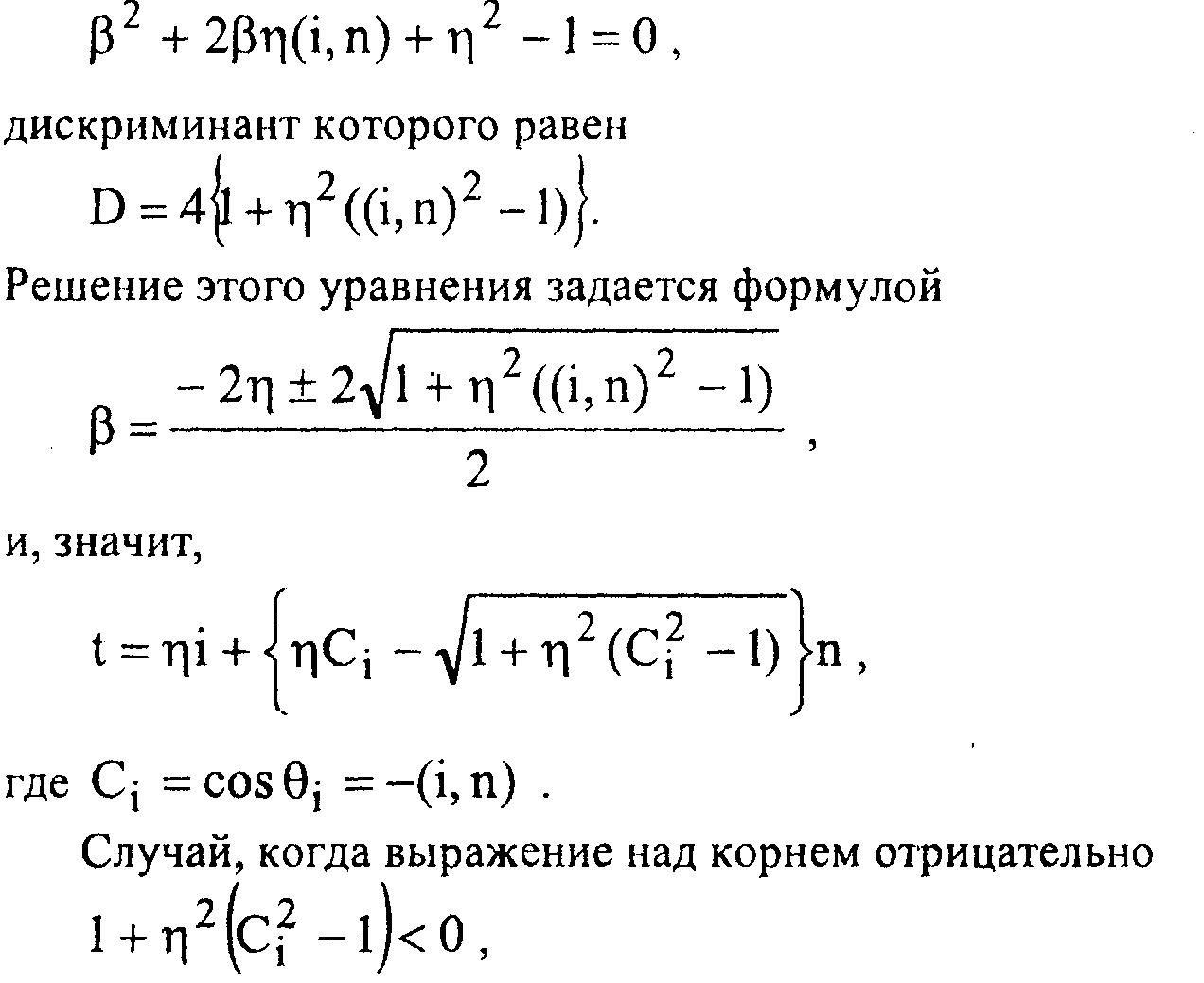
соответствует так называемому полному внутреннему отражению (вся световая энергия отражается от границы раздела сред, и преломления фактически не происходит).
2.4. Диффузное преломление Диффузное преломление полностью аналогично диффузному отражению; преломленный свет распространяется по всем направлениям 1, (1, п) < 0, с одинаковой интенсивностью.
2.5. Распределение энергии Рассмотрим теперь распределение энергии при отражении и преломлении. Из курса физики известно, что доля отраженной энергии задается коэффициентами Френеля
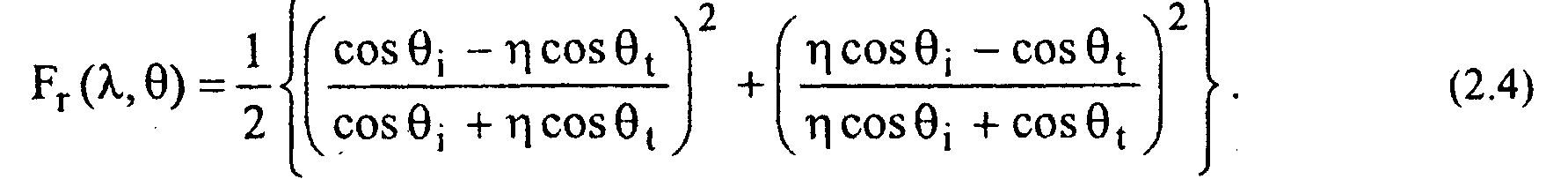
Формула (2.4) верна для диэлектрических материалов.
2. Распространение света. Освещенность
Существует и несколько иная форма записи этих соотношений:
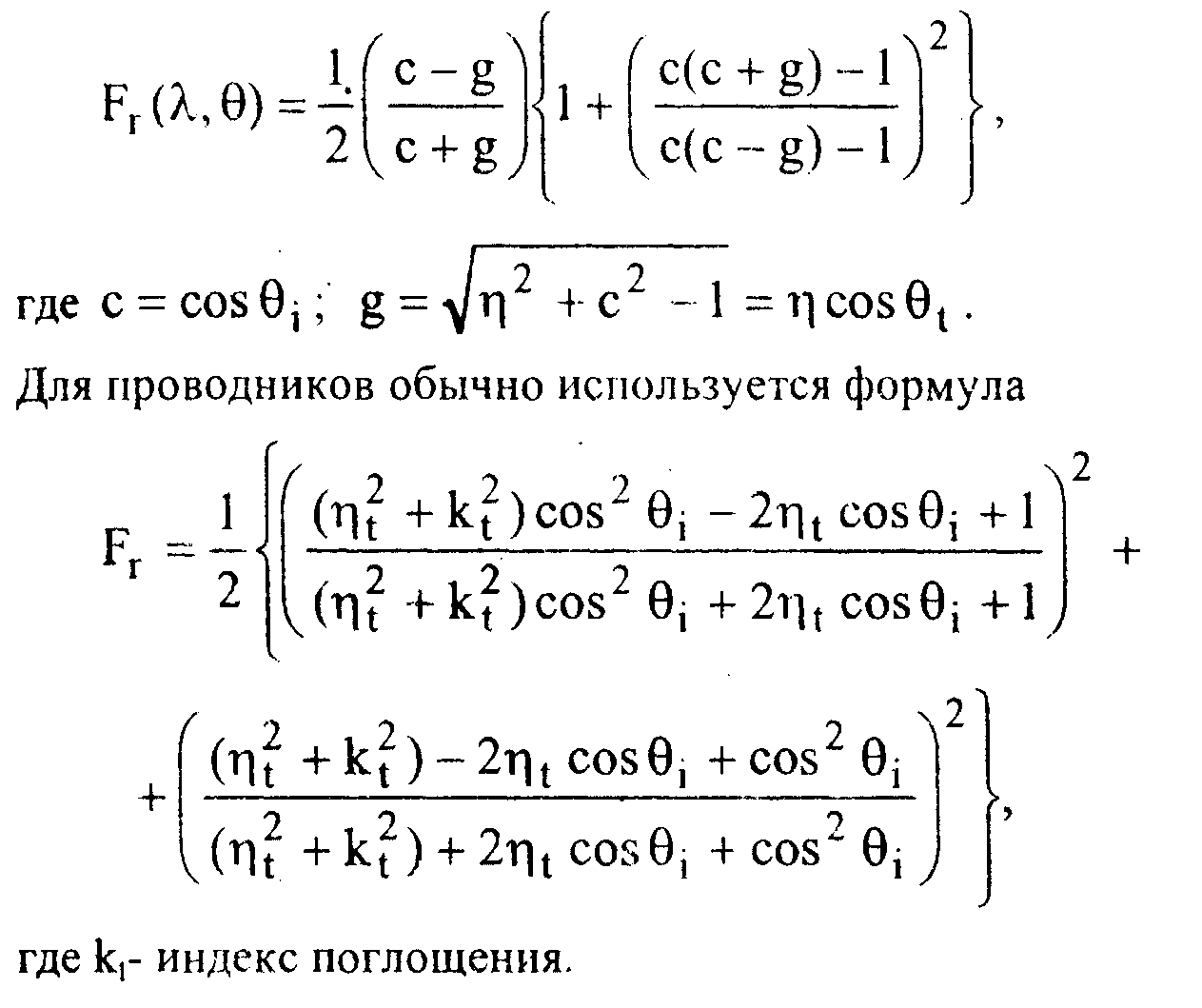
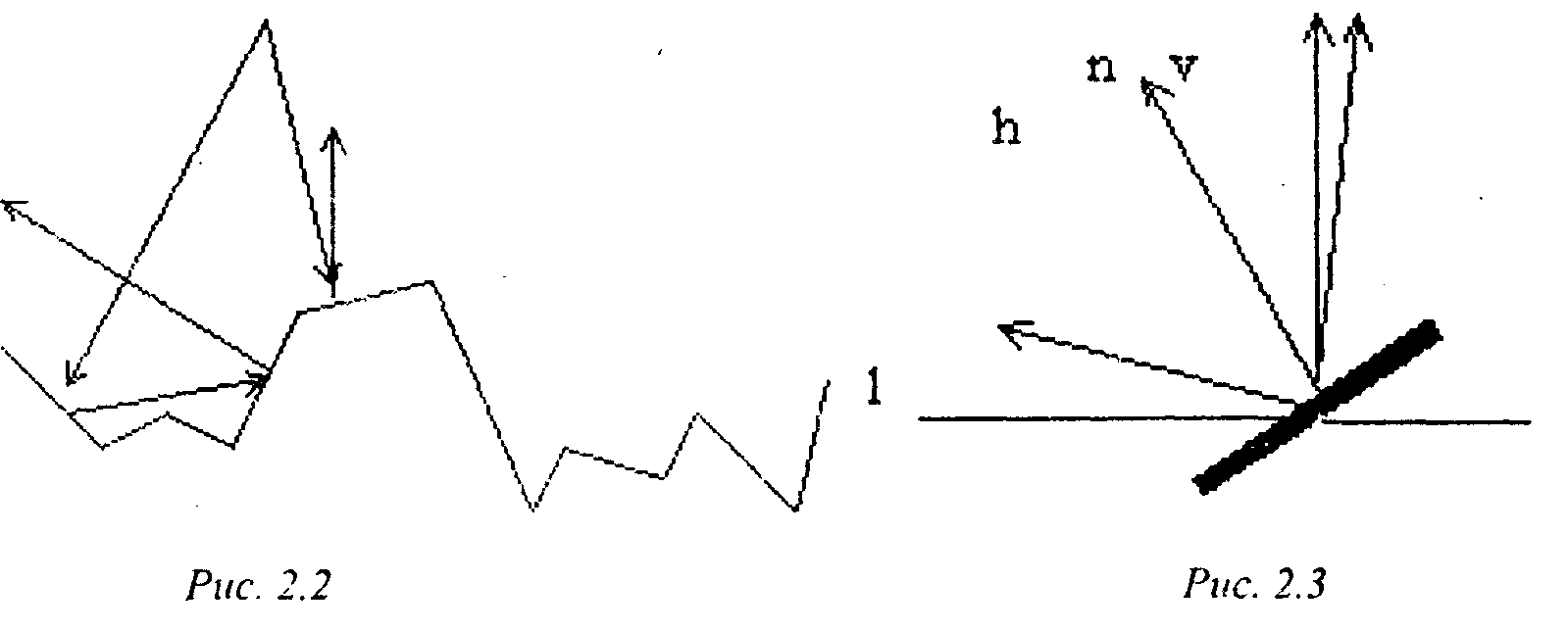
2.6. Микрофасетная модель поверхности Вес рассмотренные случаи являются идеализациями. В действительности нет ни идеальных зеркал, ни идеально гладких поверхностей. Поэтому на практике обычно считают, что поверхность состоит из множества случайно ориентированных плоских идеальных микрозеркал (микрограней) с заданным законом распределения (рис. 2.2).
Для описания поверхности, состоящей из случайно ориентированных микрограней, необходимо задать вероятностный закон, описывающий распределение нормалей этих микрограней. Каждой отдельной микрограни ставится в соответствие угол а между нормалью к микрограни И и нормалью к поверхности п (рис. 2.3), который является случайной величиной с некоторым законом распределения.
Компьютерная графика. Полигональные модели Мы будем описывать поверхность с помощью функции /)(#), задающей плотность распределения случайной величины а (для идеально гладкой поверхности функция О(а) совпадает с ^функцией Дирака).
