Существует несколько распространенных моделей. Укажем две из них: гауссово распределение:
-(-I2 0(а)=Се ^ , распределение Бекмена:
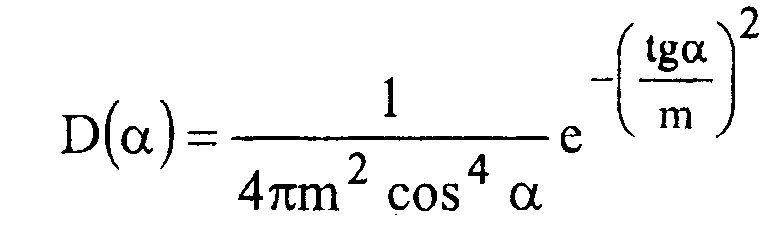
В этих моделях величина т характеризует степень неровности поверхности - чем меньше т, тем более гладкой является поверхность.
Рассмотрим отражение луча света, падающего в точку Р вдоль направления, задаваемого вектором /. Поскольку микрограни распределены случайным образом, то отраженный луч может уйти практически в любую сторону. Определим долю энергии, уходящей в направлении V? Для того чтобы луч отразился в этом направлении, необходимо, чтобы он попал на микрогрань, нормаль к к которой удовлетворяет соотношению
Доля энергии, которая отразится от* микрограни, определяется коэффициентом Френеля Рг (к, 6), где
9 = агссоз(Ь, у)= агссоБ^, 1), векторы /г, V и / единичные.
Если поверхность состоит из множества микрограней, начинает сказываться затеняющее влияние соседних граней, которое обычно описывается с помощью функции
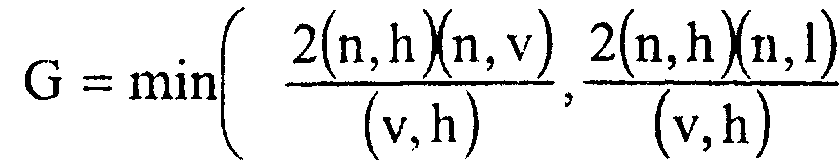
1,где п - вектор внешней нормали к поверхности.
В этом случае интересующая нас доля энергии задается формулой
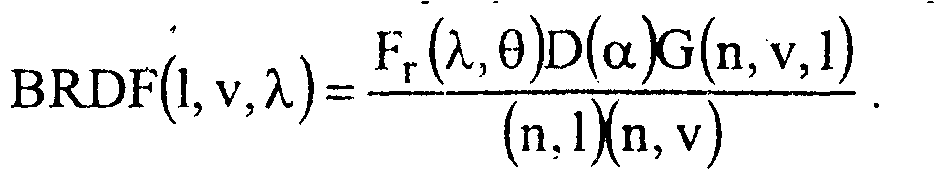
(2.5)Преломление света поверхностью, состоящей из микрозеркал, рассматривается совершенно аналогично.
2. Распространение света. Освещенность
С использованием соотношения (2.5) можно построить формулу, полностью описывающую энергию (и отраженную, и преломленную) в заданном направлении. Функция, показывающая, какая именно доля энергии, пришедшей в направлении, задаваемом вектором /, уходит в направлении, задаваемом вектором v, называется двунаправленной функций отражения (Bidirectional Reflection Distribution Function -BRDF). Для поверхностей, состоящих из множества микрограней, BRDF задается выражением (2.5).
В случае идеальной диффузной поверхности функция BRDF постоянна, а в случае идеальной зеркальной поверхности задается при помощи 5-функции Дирака.
В связи с тем что вычисление BRDF по формуле (2.5) оказывается слишком сложным, на практике обычно используются более простые формулы, например такая:
BRDF(l, v, Я.) = (n, h)k Fr (А., 9). (2.6) В общем случае BRDF удовлетворяет условию симметричности BRDF(l,v)=BRDF(v,l).
