Среда может также поглощать свет, проходящий через нее. При этом имеет место экспоненциальное затухание света с коэффициентом где / - расстояние, пройденное лучом в среде, а /? - коэффициент затухания, зависящий от среды.
При взаимодействии с границей двух сред происходит отражение и преломление света. Рассмотрим несколько идеальных моделей, в каждой из которых границей раздела сред является плоскость.
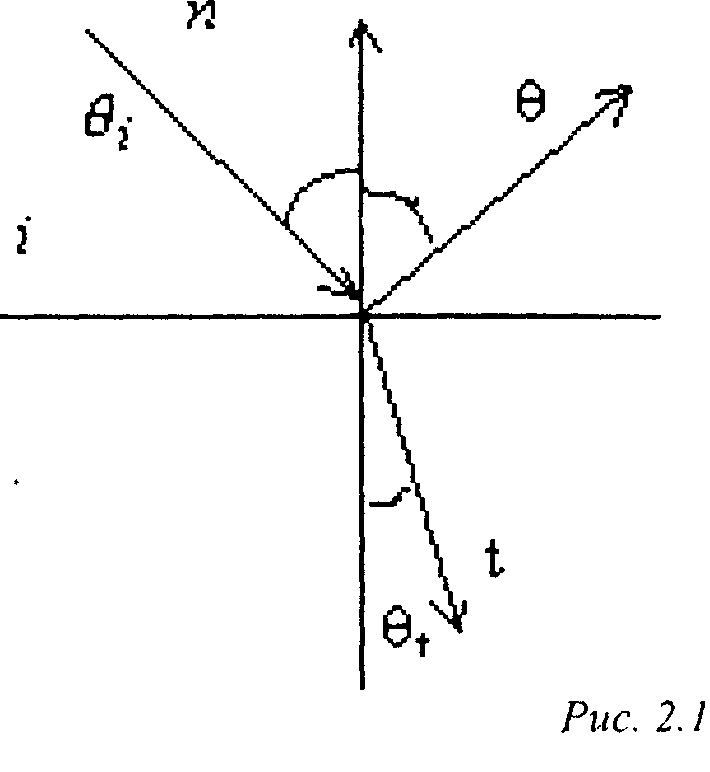
2.1. Зеркальное отражение Отраженный луч падает в точку Р в направлении / и отражается в направлении, задаваемом вектором г, который определяется следующим законом: вектор г лежит в той же плоскости, что вектор / и вектор внешней нормали к поверхности я, и направлен так, что угол падения равен углу отражения вг (рис. 2.1).
Будем считать все векторы единичными. Тогда из первого условия следует, что вектор г равен линейной комбинации векторов / и п, то есть
г = аі + Рп.
Так как 0І = 9Г, то (-і, п) = собЭ; = 0Г = (г, п). Отсюда легко получается формула г = і - 2 (і, п)п.
Вектор, задаваемый соотношением (2.1), является единичным.
(2.1)/шостш
2. Распространение света. Освещенность
2.2. Диффузное отражение Идеальное диффузное отражение описывается законом Ламберта, согласно которому падающий свет рассеивается во все стороны с одинаковой интенсивностью. Таким образом, однозначно определенного направления, в котором бы отражался падающий луч не существует; все направления равноправны, и освещенность точки пропорциональна только доле площади, видимой от источника, т. е. (/, п).
2.3. Идеальное преломление Луч, падающий в точку Р в направлении вектора /, преломляется внутрь второй среды в направлении вектора / (рис. 2.1). Преломление подчиняется закону Снел-лиуса, согласно которому векторы /, п и t лежат в одной плоскости, а для углов справедливо соотношение
r|j sinGj =r|t sin0t, (2.2)где r|j - коэффициент преломления для среды, откуда идет луч, a r\t - для среды, в которую он входит.
Найдем явное выражение для вектора /, представив его в следующем виде:
t = ori + Pn .Соотношение (2.2) можно переписать так: sin0t =r|sin0j,
