Тематическое задание 11.10. Рисование NURBS-лоскутов Уровень сложности II.
О Напишите приложение, рисующее и- и о-контуры NURBS-поверхностей, и поэкспериментируйте с ним. Ядром такого приложения является функция, вычисляющая точки на поверхности Р(и, v). Прототип такой функции может выглядеть примерно так:
Point3 nurbsPoint(Point3 Р[][]. // matrix of control points // матрица контрольных точек
int L, int M, // # of control pts - (L+DCM+l) // количество контрольных точек = (L+DCM+l)
float w[][], // vector of weights // вектор весов
Создание кривых и поверхностей
float knot[]. // knot vector // узловой вектор
int m. int n, // orders of B-splines // порядки В-сплайнов
float u. v); // values of parameters u and v // значения параметров u и v
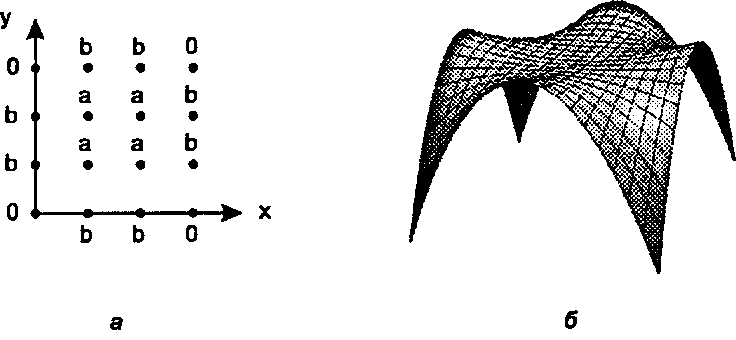
Рис. 11.69. Проектирование купола Поэкспериментируйте с контрольным полиэдром, изображенным на плоском рис. 11.69, а, где метками 0, а или Ъ отмечена высота каждой точки над плоскостью ху. На рис. 11.69, б показан пример куполообразной (domelike) формы, созданной посредством NURBS-лоскута при определенном подборе весов и высот а и Ъ. Постройте и нарисуйте лоскуты, сформированные таким способом, при задаваемых пользователем значениях а и Ъ. Испробуйте различные способы подбора весов.
1. Все веса одинаковы.
2. Всем точкам нулевой высоты присваивается вес W, а все остальные имеют вес sW, где значения коэффициента s задаются пользователем.
3. Примените другие интересные соотношения весов.
Дает ли хотя бы одна из встреченных вами комбинаций купол, близкий к полусфере? Какую корректировку нужно провести для получения купола, более похожего на полусферу?
Создайте и нарисуйте различные поверхности вращения. Как мы уже видели, поверхность вращения создается путем вращения профильной кривой вокруг какой-либо оси. Пусть наша профильная кривая лежит в плоскости xz и определена как NURBS-кривая с(и) = Щ- (1U04>
5>*"*..(«)к =0
построенная на базе набора из (L + 1) контрольных точек Qk. Мы превращаем эту кривую в поверхность вращения (ее осью вращения является ось г), объединяя ее с окружностями, перпендикулярными оси г. Окружности также определены как NURBS-кривые, поскольку эти кривые могут формировать точные конические сечения. Здесь используется NURBS-кривая на базе квадратичных сплайнов с семью контрольными точками, описанная в примере 11.9.2.
