О Покажите, что уравнение (11.92) идентично уравнению (11.91). Какое уравнение проще применить для компьютерной программы и почему?
11.11.4. Сшивание лоскутов Безье Дизайнеру может понадобиться составить сложную форму из нескольких фрагментов поверхности Безье так, чтобы эти лоскуты плавно стыковались на их общих границах. На рис. 11.56 показаны два контрольных полиэдра, черный и серый, задающие два лоскута Безье. Для обоих лоскутов используется уравнение (11.91), причем при генерировании каждого лоскута значения и\\ь изменяются от 0 до 1. Отличаются только сами контрольные полиэдры. Какие ограничения должен наложить дизайнер на эти два контрольных полиэдра, чтобы два лоскута соединились «без шва»? Нетрудно заставить два
11.11. Моделирование криволинейных поверхностей таких лоскута стыковаться во всех точках вдоль их общей границы: для этого достаточно, чтобы вдоль границы совпали их контрольные полигоны. Это так, потому что форма «границы» кривой Безье зависит только от граничного полигона контрольного полиэдра. (Посмотрите, что произойдет, если в уравнении (11.91) положить и = 0.) Поэтому дизайнер выбирает для двух лоскутов одинаковые контрольные полигоны.
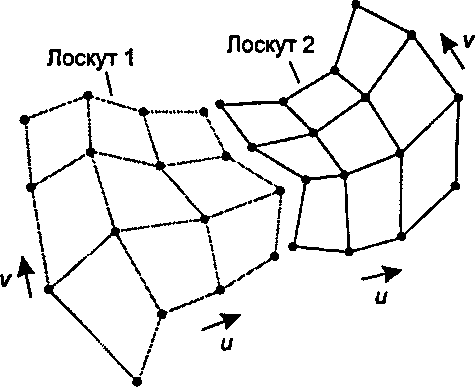
Рис. 11.56. Непрерывная стыковка двух лоскутов Безье Сложнее добиться непрерывности касательной в месте соединения двух лоскутов. Однако если эта непрерывность будет обеспечена, то будет гарантирована также непрерывность нормали к поверхности в месте соединения. Один вариант достаточного условия [Faux, 61] приводится на рис. 11.57"images/tmp8E4A-817.png" alt="Обеспечение непрерывности касательной по границе Пример 11.11.2. Создание ручки чайника">
Рис. 11.57. Обеспечение непрерывности касательной по границе Пример 11.11.2. Создание ручки чайника Мы уже видели, что корпус и крышка чайника, показанные на рис. 11.53, являются поверхностями вращения на базе кривых Безье. С другой стороны, и ручка, и носик состоят из четырех лоскутов Безье. В этом примере мы покажем, как конструируется ручка, а носик рассматривается в тематическом задании 11.8.
