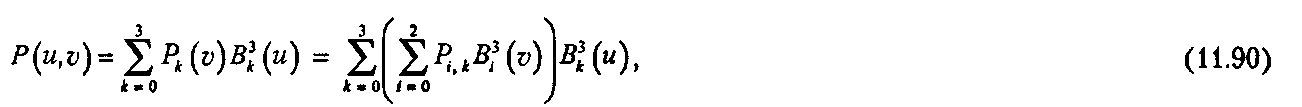
где и и v, как обычно, изменяются от 0 до 1. Пример такого лоскута приведен на рис. 11.54. Каждый ^-контур, например при v = v0, является кривой Безье относительно ы на базе четырех контрольных точек Pk(v0), которые сами лежат вдоль квадратичных кривых Безье. (Как описывается каждый ы-кон-тур?) Все 12 контрольных точек PiV образуют контрольный полиэдр (control polyhedron), определяющий форму данного лоскута. Такой способ задания поверхности называется формой тензорного произведения (tensor product).
Рис. 11.54. Пример лоскута Безье В общем случае контрольный полиэдр является каркасом (network) из (М + 1)(I + 1) вершин, а выражение для поверхности имеет вид:
PM-tlntf (И.91)
* = 0 i = 0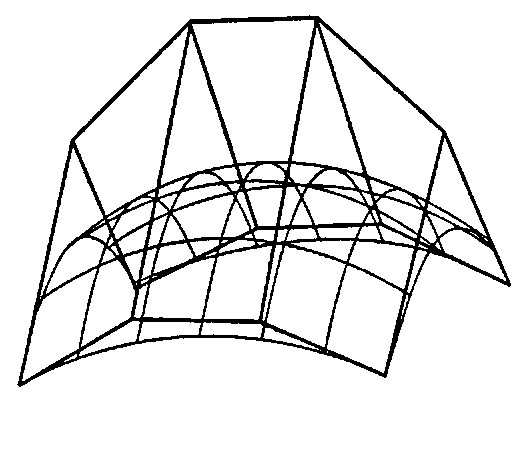
Создание кривых и поверхностей
Для формирования лоскута дизайнер тщательно задает позиции этих вершин и затем при помощи уравнения (11.91) определяет форму поверхности. В упражнениях ниже рассматривается альтернативная матричная форма поверхности Безье.
На рис. 11.55 приводится пример бикубического (bicubic) лоскута Безье (здесь L = М = 3) и его контрольный полиэдр. За дальнейшими подробностями по поводу кривых Безье обращайтесь к работе [Rogers, 174].

Рис. 11.55. Бикубический лоскут Безье и его контрольный полиэдр
Практические упражнения
11.11.1. Восстановление промежуточной формы
Как составить контрольный полиэдр, используемый в уравнении (11.91), чтобы осуществлялась линейная интерполяция между двумя контрольными полигонами?
11.11.1. Нормали к лоскутам Безье Используя в уравнении (6.25) параметрическую форму лоскута Безье, выведите (сложное) выражение для нормального вектора к этому лоскуту. Упростите полученное выражение, насколько это возможно. При всех ли значениях (и, о) нормальный вектор изменяется непрерывно?
11.11.3. Альтернативная форма лоскута Безье Следующая форма бикубической (7. - М - 3) поверхности Безье поможет продемонстрировать совместное поведение ее частей"images/tmp8E4A-815.png">
(11.92)Внешние пары векторов и матриц создают полиномы Бернштейна, а внутренняя матрица содержит геометрию лоскута.
О Сравните уравнение (11.92) с аналогичной формой кривых Безье, определяемой уравнением (11.41).
