Р(и, v) - (X(»)cos(m), X(»)sin(m), Z(v)). (11.88)
Часто бывает удобно выразить профиль, используя кривые Безье или В-сплайн кривые. Выберем L + 1 контрольных точек (Хк, Zk) и на базе их сформируем кривую:
(x(v),Z(v))= £(^,7,)^,». (11.89)к = 0
На рис. 11.52, а показан профиль кубка, заданный в форме В-сплайн кривой, а также контрольный полигон. На рис. 11.52, б приводится результирующая поверхность вращения. (Каркасный объект для данной поверхности вращения создавался так же, как в главе 6, а сама сетка рисовалась при помощи метода Mesh :: drawO.)
Создание кривых и поверхностей
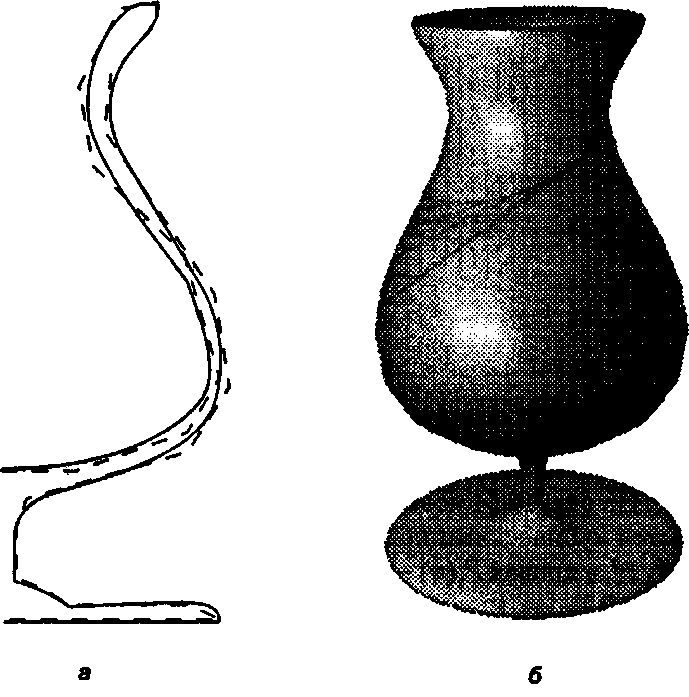
Рис. 11.52. Профиль в виде В-сплайн кривой: а) профиль: В-сплайн кривая; б) кубкообразная поверхность вращения Пример 11.11.1. Классический чайник Для создания профилей можно использовать также кривые Безье. На рис. 11.53, а показан профиль корпуса «чайника», впервые сконструированного Мартином Ньюэллом (Martin Newell) [Blinn, 24, Crow, 54]. Корпус чайника изображен на рис. 11.53, б. Профиль корпуса состоит из трех кривых Безье на базе 10 точек, представленных в табл. 11.1. Первая кривая Безье определяется точками 0,1,2,3; вторая - точками 3,4,5,6, а третья - точками 6,7,8,9. Отметим, что последний сегмент каждой кривой колли-неарен первому сегменту следующей кривой. Это условие гарантирует, что сопряжение различных кривых Безье происходит с G'-непрерывностью (см. раздел «Плавность движения» данной главы) Крышка чайника также является поверхностью вращения; она рассматривается в тематическом задании 11.8.
Таблица 11.1. Данные для профиля корпуса чайника
| i | X | z |
| 1,4 | 2,25 | |
| 1,3375 | 2,38125 | |
| 1,4375 | 2,38125 | |
| 1,5 | 2,25 | |
| 1,75 | 1,725 | |
| 1,2 | ||
| 0,75 | ||
| 0,3 | ||
| 1,5 | 0,075 | |
| 1,5 |
11.11. Моделирование криволинейных поверхностей
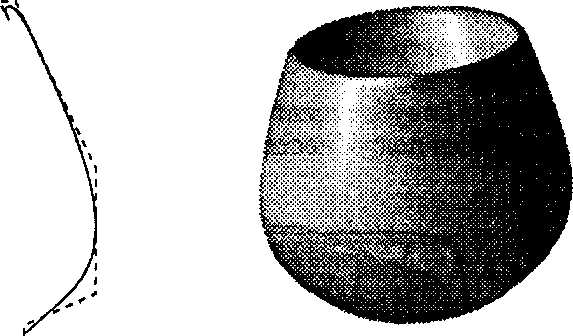
а б Рис. 11.53. Профили для корпуса чайника на основе кривых Безье: а) профиль корпуса; б) чайник
11.11.3. Лоскуты Безье На рис. 11.51 показан фрагмент (лоскут) линейчатой поверхности на базе двух кривых Безье. Для большей гибкости проектирования можно заменить линейные ы-контуры из уравнения (11.87) на кривые Безье или В-сплайн кривые. В лоскуте Безье как для и-, так и для ^-контуров применяются кривые Безье. Если, например, ы-контуры являются квадратичными кривыми Безье, а о-контуры - кубическими кривыми Безье, то соответствующий лоскут Безье может быть представлен в следующем виде:
