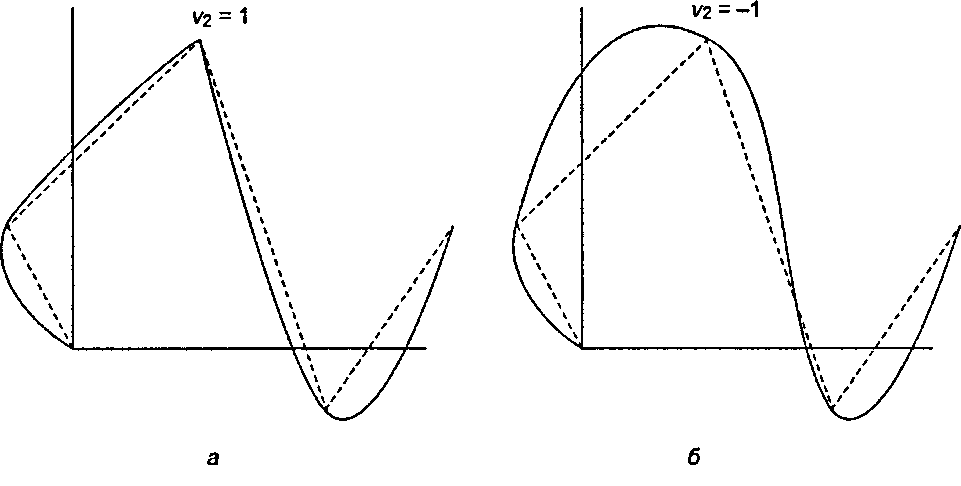
Рис. 11.46. Влияние натяжения в вершине 2: а) натяжение = 1; б) натяжение = -1
Дополнительный контроль смещенности В классе кривых, известных как сплайны Кочанека-Бартелса (Kochanek-Bartels splines), содержатся и другие параметры, предназначенные для лучшего манипулирования формой кривой [Kochanck, 126]. Одним из этих параметров является «смещенность» (bias). Отметим, что при т = 1/2 уравнение (11.80) может быть записано в виде:
?'(1к) = ^(Рк-Рк.,)+1-(Рк^-Рк), (11.82)
что представляет собой среднее значение двух соседних векторов Рк - Рк , и Pkt, - Рк. (Посмотрите это на рис. 11.44.) Параметр смещенности Ьк неодинаково взвешивает два вышеприведенных компонента согласно формуле
Создание кривых и поверхностей
Р'(0 = 1{\-Ьк){Рк-Рк.х) + L(l+bk)(Pk + l-Pk), (11.83)
так что фактическая скорость, задаваемая в точке соединения, определяется одним соседним вектором в большей степени, чем другим. При Ьк - 0 оба этих вектора взвешены одинаково. На рис. 11.47 показан эффект от смещенности в вершине Р2 для кривой с рис. 11.45.
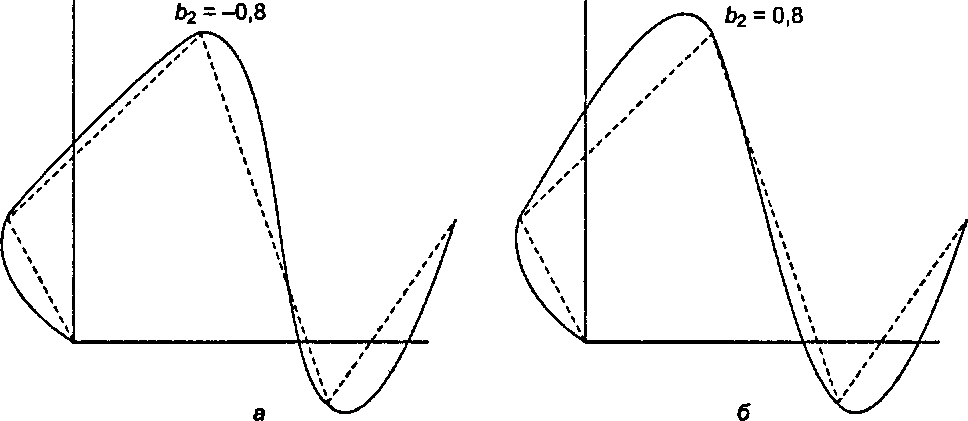
Рис. 11.47. Эффект от смещенности в вершине 2: а) натяжение = -0,8; б) натяжение = 0,8
Добавление управления непрерывностью
Вместо требования непрерывности скорости в точке Рк Кочанек и Бартелс (Kochanek and Bartels) вводят другой параметр, призванный предоставить дизайнеру возможность сделать скорость «непосредственно перед» стыком отличной от скорости «непосредственно за» ним. Рассмотрим соединение в точке Рк. (Jt - 1)-й сегмент Rk_,(t) (см. уравнение (11.74)) достигает точки Рк при г = 1. Скорость на этом сегменте при с - 1 зададим следующим образом:
^.,(1) = 1(1-Ск)(Рк-Рк.{) + \(1+ск)(Рк + 1-Рк), (11.84)
где ск- параметр непрерывности (continuity parameter). (Здесь уравнение выглядит точно так же, как и в случае параметра смещенности: большие значения ск смещают скорость в сторону вектора Рк+1- Рк) Аналогично k-ii сегмент Rk(t) выходит из точки Рк при г - 0. Его скорость в этот момент времени зададим формулой
r;(0) = |(l + c4)(/J-/»,_,) + \(l-ck){Pk + l-Pt), (11.85)