РЧд-шСР^.-Р,.,), (11.80)
где т - некоторый скаляр. (Ниже мы рассмотрим влияние коэффициента т; часто принимают т=1/2.). В терминах предыдущих величин данное условие задает наклон г/-компонеита следующим образом: ^ * т(ук+, - ук_,); аналогичное выражение может быть получено и для дс-компонента.
Поскольку мы задали значения наклонов 54 для каждой внутренней точки соединения, теперь можно определить коэффициенты различных кубических полиномов в уравнении (11.74) для к - 1,…, Ь - 2. Нам по-прежнему требуются два дополнительных условия для задания еще не определенных наклонов на концах $0 и 5£ _С этой целью можно использовать то же самое условие равенства нулю вторых производных на концах, что приводит нас к уравнению (11.78). В упражнениях рассматриваются и другие возможности. На рис. 11.45 показан пример кривой, сгенерированной с помощью этого метода.
Добавление управления натяжением С целью предоставления дизайнеру большего контроля над формой кривой в каждой точке соединения в методе Кэтмулла-Рома вводится параметр «натяжения» ьк. Этот параметр обеспечивает дизайнеру управление константой тп в уравнении (11.80) путем изменения величины скорости Р'(г) в точке соединения без изменения ее направления. Согласно этому методу, скорость в к-н точке соединения равна р'(0=1(1-гО(р4+1-ра..,), где А " 1,…, 1,-1. (Чему в этом случае равняется наклон 54?)
(11.81)11.10. Краткое знакомство с интерполяцией
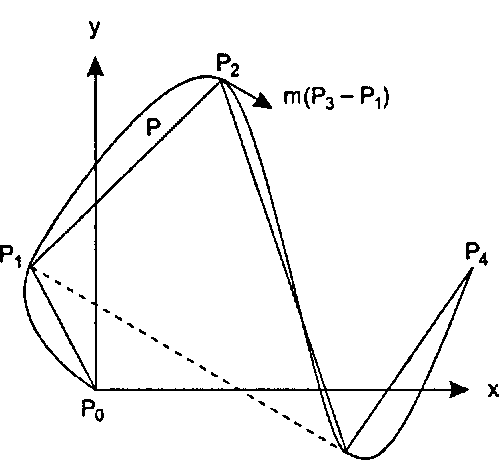
Рз Рис. 11.45. Интерполирующая кривая на базе сплайна Кэтмулла-Рома (при m = 1/2)
Хотя обычно натяжение vk задается в диапазоне от -1 до 1, оно может принимать и любое другое значение. Случай vk = 0 соответствует значению т - 1/2, согласно уравнению (11.80). На рис. 11.46 показано влияние натяжения в вершине Р2 на форму кривой. На рис. 11.46, а натяжение v2 равно 1, поэтому скорость в точке соединения также стала нулевой. Это выпрямляет кривую при ее приближении к стыку. (Почему?) На рис. 11.46, б v2 равно -1, поэтому кривая в точке соединения выглядит более «расслабленной».
