Листинг 11.2. Этап прямого исключения v[0] - 0.25:
q[0] = 3.0 * (у[1] - у[0]) * v[0]:
ford - 1; i < L: i++)
{
v[i] = 1.0 / (4.0 - v[i - 1]):
q[i] - (3.0 *(y[1]-y[i-l]) - q[1 - 1]) * v[1]:О Покажите, что код из листинга 11.2 действительно осуществляет прямое исключение на базе массивов v[] и q[].
О Для получения искомых значений s[] выполняется этап обратной подстановки (backward-substitution). В крайнем правом столбце матрицы из уравнения (11.79) содержится единственный ненулевой элемент, поэтому sA " gA. Покажите при помощи нижеприведенного фрагмента кода, что, двигаясь обратно по уравнениям, можно получить любое значение s:
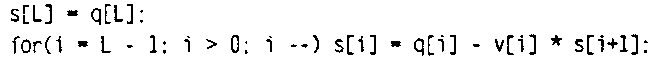
11.10.4. Вычисление наклонов при кубической интерполяции Существует еще несколько методов задания наклонов кривых в местах соединения. Рассмотрим вкратце наиболее популярный из них: семейство сплайнов Кэтмулла-Рома (Catmull-Rom)1 [Bartels, 126; Farin, 60] и их вариации. Мы по-прежнему хотим, чтобы кривая была 1-гладкой во «внутренних» точ1 Иногда эти сплайны называют фундаментальными (cardinal), а иногда - сплайнами Оверхаузера (Overhauser). Фактически все они являются частными случаями более общего семейства кривых Кэтмулла-Рома.
Создание кривых и поверхностей
ках соединения, однако теперь отказываемся от требования ее 2-гладкости в этих точках. Можно ожидать, что отказ от дополнительной степени гладкости предоставит дизайнеру больший локальный контроль над формой кривой. В противоположность заданию значений наклонов 54 с целью обеспечить непрерывность второй производной теперь мы зададим эти наклоны исходя из координат соседних с ними контрольных точек.
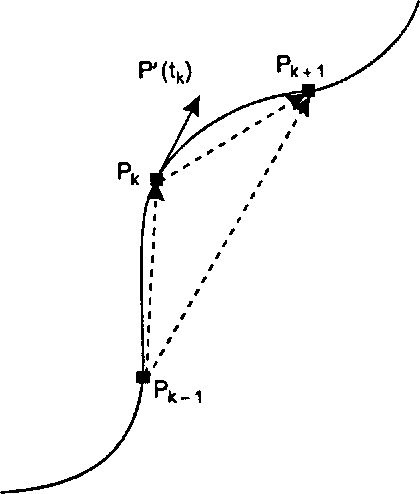
Рис. 11.44. Задание наклонов на основе значений соседних контрольных точек Простейший метод Кэтмулла-Рома состоит в присвоении вектору скорости в точке Рк величины Р'(г4) на базе координат двух соседних точек. Как показано иа рис. 11.44, этот вектор принимается просто пропорциональным вектору, соединяющему точки Рк_, и Рк+В результате этого направление кривой в точке Рк станет параллельным отрезку, соединяющему предыдущую и последующую точки. Таким образом, потребуем, чтобы
