2*0 + 5, - 3(у, - у0);
25, + 51.,-3(у1-у1.1). (11.78)
Уравнения (11.76) и (11.77) представляют в совокупности 1+1 линейное уравнение относительно неизвестных наклонов 54. Как будет показано в упражнениях, структура этих уравнений довольно проста для решения.
На рис. 11.43 приведен набор контрольных точек и интерполирующий их естественный кубический сплайн. Отметим, что на вид эта кривая повсюду выглядит гладкой, причем на концах кривая выпрямляется так, что вторая производная обращается в нуль. Пунктирной линией показан эффект от смещения одной из контрольных точек. Форма кривой изменилась везде; таким образом, естественные сплайны не обеспечивают локального контроля, поскольку требование непрерывности второй производной «связывает» производные первого порядка в узлах и изменение одной производной вызывает сквозное возмущение всех остальных.
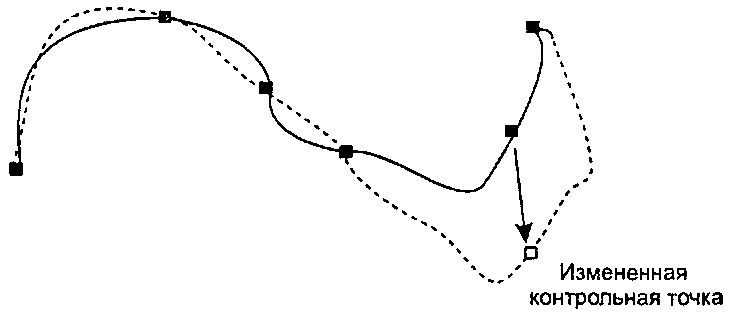
Рис. 11.43. Естественные кубические сплайны, интерполирующие контрольные точки Практическое упражнение
11.10.4. Решение уравнений для наклонов естественного сплайна Уравнения (11.76) и (11.77) более наглядны в матричной форме. Для случая Ь
= 4 имеем"images/tmp8E4A-799.png">
Эта матрица является тридиагональной (tridiagonal): ее ненулевые члены сосредоточены на трех диагоналях. Это позволяет решать данную систему уравнений в два простых этапа, описанных ниже.
О Пройдем систему уравнений методом прямого исключения (forward-elimination) для аннулирования единиц в верхней диагонали. Для этого разделим первое уравнение на 2, вследствие чего его первый элемент превратится в 1. Затем, начиная со второго уравнения, вычтем поочередно из каждого уравнения соответствующую «долю» предыдущего уравнения для исключения 1, после чего промасштабируем уравнение так, чтобы на диагонали стояла единица. Покажите, что такой процесс преобразует систему уравнений к «нижней диагональной» форме (когда выше главной диагонали располагаются только нули):
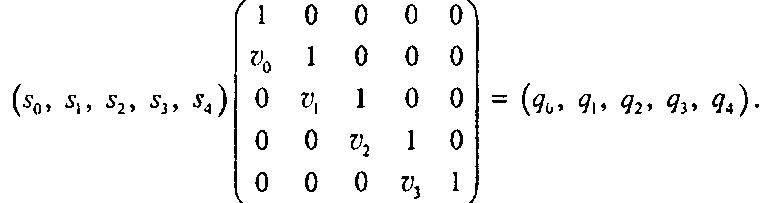
(11.79)Кроме того, покажите, как просто вычислить члены vi и q{.
