При S = 0 в месте соединения образуется угол (см. нижеследующие упражнения). Скорости обеих кривых R0(t) и Rt(t) при приближении к стыку стремятся к нулю, поэтому хотя скорость всей кривой резко изменяет направление в точке соединения, кривая тем не менее остается 1-гладкой. (Является ли эта кривая С-непрерывной?)
Практические упражнения
11.10.1. Когда скорость нулевая Пусть скорость сегмента кубической кривой равна нулю на обоих концах. Покажите, что этот сегмент является прямой линией.
11.10.2. Исследование кривых
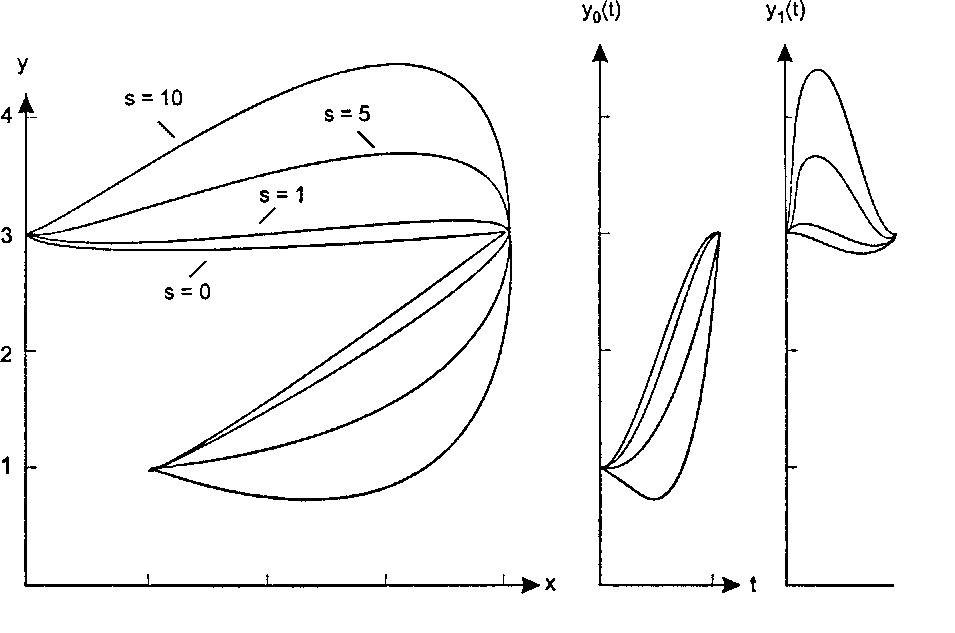
Напишите короткую программу, которая генерирует кривые, изображенные на рис. 11.41 и 11.42, и прогоните эту программу при различных значениях 5. Для лучшего выполнения программы рекомендуем определить следующую функцию для у:
Point2 y(float t. float S. int seg) {
double t2 - t * t. t3 = t2 * t: return (seg == 0)?
(S-4) * t3 + (6 - S) * t2 + 1:
(S+l) * t3 -(2 * S + 1) * t2 + S * t + 3:
}и аналогичную функцию для х.
11.10.3. Создание петли Покажите, что при S = -1 кривая с рис. 10.41 имеет петлю.
Создание кривых и поверхностей
11.10.3. Естественные кубические сплайны
В качестве одного из способов задания значений производных 54 при формулировке Эрмита используем такие значения 54, при которых вторая производная от у(£) будет непрерывной на каждом из «внутренних» стыков, где к - 1, 2,…, Ь- \. (На «концах» всей кривой производным пет необходимости быть непрерывными.) Вторая производная на каждом сегменте равна у"(£) = &акЬ + 2Ьк, поэтому, приравнивая 7Г-1О) к У' (0). получим:
6ак_,+2Ьк_1~2Ьк, (11.76) где* - 1,2.....1-1.
Используя значения коэффициентов из уравнения (11.74), после упрощений получим следующее условие для наклонов: где к" 1, 2,Ь - 1. Из этого уравнения видно, как должны быть связаны соседние наклоны, чтобы обеспечить непрерывность второй производной во внутренних точках соединения. Нам все еще остается задать первый и последний наклоны - $0 и 5г При традиционном подходе они выбираются так, чтобы на обоих концах кривой вторые производные равнялись нулю; то есть у'' (0) = 0 и у"_х (1) = 0. Из первого условия следует, что Ь0 = 0, а из второго - Ъаь _, + Ь1 _, - 0. (Почему?) Снова используя уравнение (11.74), получим два последних условия:
