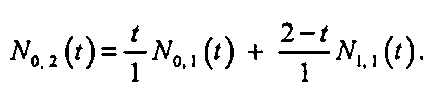
(11.60)Мы видим, что линейный «подъем» (up ramp) (задаваемый членом г) умножается на ДО0 ,(г), а линейный «спуск» (down ramp) (2 - г) умножается на ДО, ,(г), как показано на рис. 11.28, а. В результате суммирования этих членов получается треугольный импульс (pulse, рис. 11.28, б). Отметим имеющуюся здесь аналогию с твинингом: N02(t) является аффинной комбинацией ДО0,(t) и ДО, ,(г). Тогда ДО0 2(г) равно г при 0 й t < 1, равно 2-е при 1 < г < 2 и равно нулю в остальных случаях.
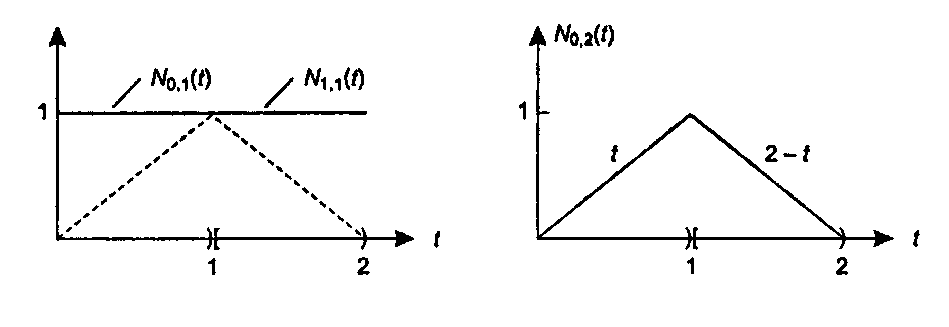
а б Рис. 11.28. Построение линейных В-сплайнов Построение других линейных В-сплайнов производится аналогично. Например, ДО, 2(г) - это треугольный импульс, начинающийся при г - 1 и заканчивающийся при г=3: он является просто смещенной версией предыдущего импульса. Вообще говоря, при равноотстоящих узлах любой линейный сплайн является смещенной версией нулевого сплайна; то есть ДО; 2(с) - Ы0 2(с -1).
Если нарисовать несколько функций ДО4 2(с), то становится очевидным, что импульсы перекрывают друг друга как раз таким образом, что их сумма при любом с равна единице. (Проделайте это!)
Отметим, что кривая, построенная на линейных В-сплайнах, совпадает с контрольной ломаной линией. (Сохраняется ли это в случае, когда узлы не эквидистантны?) Поскольку линейные сплайны не могут предложить ничего, кроме обычных прямых линий, то обычно их не используют для дизайна кривых. Однако они, разумеется, фигурируют в процессе построения В-сплайнов более высоких порядков.
11.7. Базисные функции В-сплайнов Пример 11.7.2. Квадратичные В-сплайны
Предположим, что мы хотим определить форму квадратичных (т = 3) В-сплайн функций N. 3(с) на базе тех же равноотстоящих узлов, что и в предыдущем примере. Тогда нам нужно построить только функцию ЛГ0 3(0, так как остальные функции могут быть получены из этой простым смещением. Из уравнения (11.58) видно, что
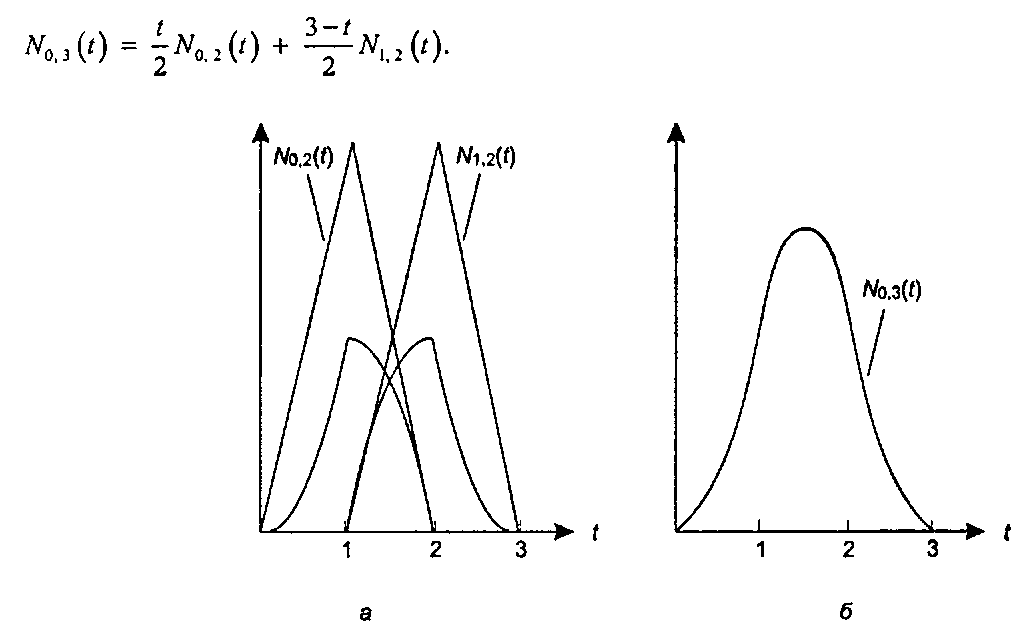
Рис. 11.29. Форма первого квадратичного В-сплайна
(Отметим, что снова происходит твининг двух сплайн-функций более низкого порядка.) Первый член - это произведение подъема на первый треугольный импульс, а второй член - произведение спуска на второй импульс. Как показано на рис. 11.29, а, произведения подъема и спуска на треугольные импульсы представляют собой две параболы, пересекающиеся под углом. Однако когда два соответствующих члена уравнения (11.61) складываются, углы исчезают и результирующий импульс ЛГ0 3(г) (рис. 11.29, б) имеет непрерывную производную.
