Уравнение (11.61) можно использовать для определения алгебраического выражения квадратичного сплайна для каждого сегмента. В среднем сегменте содержится сумма двух квадратичных полиномов, а общий результат имеет вид:

(11.62)Отметим, что N0 з зависит от четырех узлов 0, 1, 2,3, а его поддержкой является промежуток [0,3].
Сравнивая N0 3(г) cg(t) из уравнения (11.49), мы видим, что они в точности совпадают. Это вызвано тем, что в качестве g(t) была (намеренно) выбрана именно В-сплайн функция. В результате проверки мы уже убедились, что ее первая производная непрерывна. Однако вторая производная - нет. Таким образом, квадратичные В-сплайны (по крайней мере, при равноотстоящих узлах) действительно являются сплайнами.
Создание кривых и поверхностей
Другие формы квадратичных сплайнов, например 3(с), для случая равноотстоящих узлов могут быть легко получены. Поскольку сплайны первого порядка являются просто собственными смещенными версиями и поскольку все возрастающие члены уравнения (11.58) содержат только разности узловых значений, то квадратичные сплайны также должны быть просто собственными смещенными версиями. В действительности это имеет место для В-сплайна любого порядка при равноотстоящих узлах: Если Ск - к, то ^ и(0 = ЛГ0 и(с - к). (11.63)
Если узлы эквидистантны, то это выражение можно непосредственно подставить в уравнение (11.57).
Ранее мы утверждали, что квадратичные сплайны из уравнения (11.58) при любых значениях с в сумме равны единице. В упражнениях в конце раздела будет показано, что это верно даже в случае неравноотстоящих узлов.
Пример 11.7.3. Кубические В-сплайны
Кубический В-сплайн - это, вероятно, наиболее часто используемый вид В-сплайна. На рис. 11.30, а показан вид сплайна ДО0 4(г) для равноотстоящих узлов. Его формула может быть найдена тем же способом, что и раньше. (См. упражнения.). Сплайн ЛГ0 4(г) симметричен относительно точки с - 2; его компактное выоажение выглядит так:
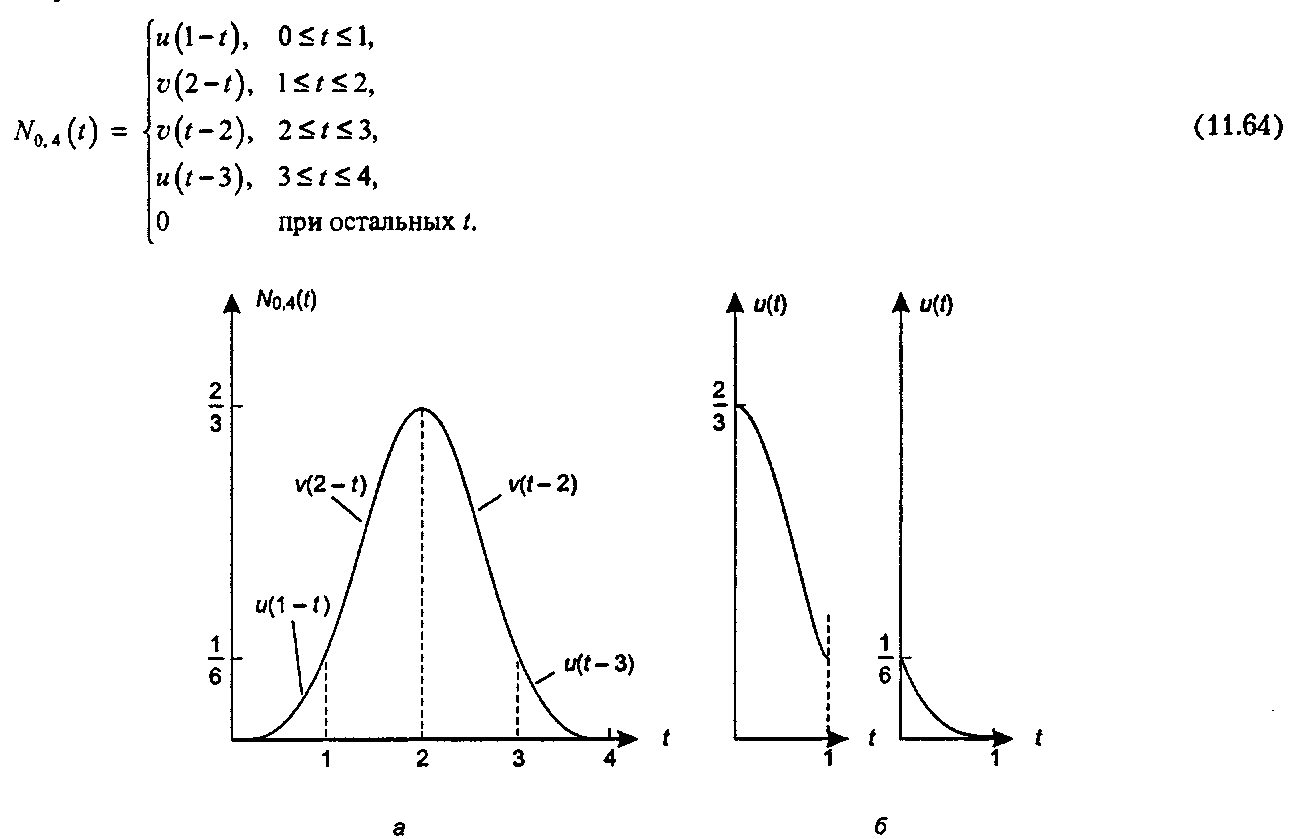
Рис. 11.30. Кубический В-сплайн для равноотстоящих узлов Два элемента этой формулы - функции м( ) и ь( ), изображенные на рис. 11.30, б, - имеют следующий вид"opengl1_792.html">⇐ Предыдущая| |Следующая ⇒
