Каждая В-сплайн функция базируется на полиномах определенного порядка т. Если т = 3, то полиномы будут иметь порядок 3 и, следовательно, степень 2, то есть будут являться квадратичными В-сплайна-ми. Если т - 4, то соответствующие полиномы будут иметь степень 3, то есть будут кубическими. Эти два случая наиболее важны, хотя обсуждаемая формула позволяет строить В-сплайны любого порядка.
11.7.1. Определение В-сплайн функций Полезно в обозначении В-сплайн функции указывать ее порядок в явном виде, то есть вместо того, чтобы писать просто Rk(t), мы будем обозначать стыковочную функцию В-сплайна т-то порядка символом Nkm(t). Тогда уравнение (11.54) для В-сплайн кривой примет вид:
/>(/) = £ЗД.Л')- (11.57)
*ж0
Систематизируем все, что мы имеем на данный момент: О узловой вектор Т - (г0, с,, с2,… ); О (I + 1) контрольных точек Рк; О порядок m В-сплайн функций.
1 Обращаем внимание на различие между сплайн-функцией, определенной в разделе «Кусочно-полиномиальные кривые и сплайны», и сплайн-кривой. Сплайн-функция - это обычный кусочный полином с определенной степенью гладкости. Сплайн-кривая - это аффинное сопряжение точек, в котором используются кусочно-полиномиальные функции сопряжения. Сплайн-кривая должна быть непрерывной в своих узлах, однако производные в узлах могут терпеть разрывы.
Создание кривых и поверхностей
Основная формула, описывающая В-сплайн функцию ДО^ т(с), имеет следующий вид:
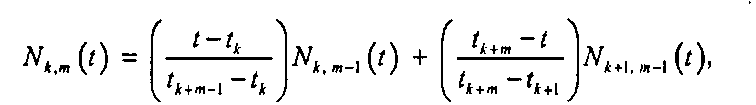
СИ.58)
где к - 0, 1,…, Ь. Такое определение является рекурсивным и описывает построение функции тп-го порядка из двух В-сплайн функций (т - 1)-го порядка. Для инициализации этой формулы мы должны определить функцию первого порядка. Это просто постоянная единичная функция в пределах своего диапазона:
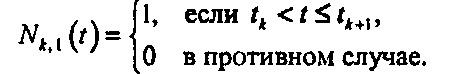
Отметим, что сумма такого набора функций автоматически равняется единице для всех значений г; следовательно, при формировании комбинаций из точек использование таких функций допустимо.
Пример 11.7.1. Линейные В-сплайны
Какую форму имеет функция ДО0 2(г), первая (£ = 0) В-сплайн функция порядка т - 2, если все ее узлы - равноотстоящие (то есть вектор Т = (г0 - 0, с, - 1, с2 - 2,…))? При этих значениях параметров уравнение (11.58) приобретает вид:
