путем смещения функции g(.) на целые величины:
&(0-£(*-*), гае*-0,1..... (11.50)
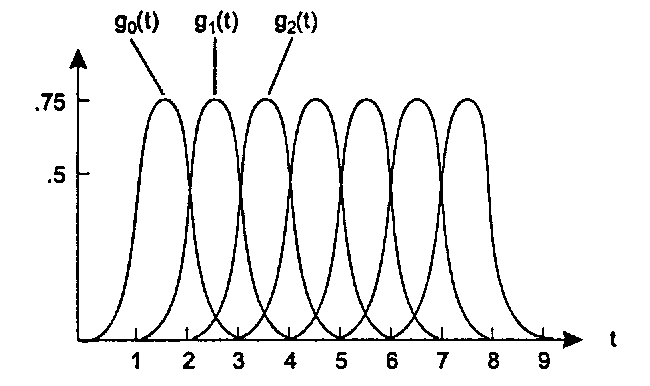
Рис. 11.24. Замкнутые кривые на основе сплайнов Поскольку узлы различных версий £(.) являются целыми числами, смещение функции £(.) на целое число равносильно такому перемещению, что узлы одной смещенной версии совпадают с узлами следующей версии. Такие смещенные версии образуют допустимый набор стыковочных функций, только если при каждом £ их сумма в точности равна единице. В действительности это выполняется для всех I в пределах от 2 до 7! (См. упражнения в конце раздела.) Это означает, что
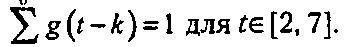
(11.51)Такое смещение может показаться магическим, однако мы увидим, что это общее свойство всех стыковочных функций, которые мы в конечном счете разработаем. Чрезвычайно важно, что мы смещаем каждую функцию на целое число единиц с целью «выровнять» их так, чтобы их сумма составляла единицу.
Итак, дизайнер выбирает семь контрольных точек и генерирует кривую с помощью следующего алгоритма"images/tmp8E4A-770.png">
Создание кривых и поверхностей
троль над формой кривой. Кроме того, отметим, что в моменты времени г - 2,3,…, 7 активны только две функции, причем обе они равны 0,5. Поэтому при этих значениях с функция У(г) будет лежать посередине прямой, соединяющей две контрольные точки.
На рис. 11.25 приведен пример расположения семи контрольных точек вместе с результирующей кривой. Эта кривая начинается при г - 2 в средней точке отрезка Р0Р{ и, плавно изгибаясь, проходит через последующие средние точки ребер контрольного полигона. По мере возрастания г включаются и выключаются различные стыковочные функции, и главное влияние на кривую «передается» от точки к точке.
Какими свойствами обладают кривые на базе такого набора стыковочных функций? О Дизайнеру предоставляется некоторый локальный контроль над формой кривой, поскольку интервал поддержки каждой стыковочной функции ограничен длиной в 3 единицы.
