О Дизайнер будет задавать точки, осознавая то обстоятельство, что кривая должна пройти через середины ребер контрольного полигона. Поэтому алгоритм обладает некоторыми интуитивными геометрическими свойствами.
О Поскольку каждая стыковочная функция 1-гладкая, то вся кривая также 1-гладкая.
О Ни одна из точек на кривой не интерполируется.
О Все полиномы имеют вторую степень, поэтому их вычисление отличается быстротой и устойчивостью. Степень полиномов не зависит от числа контрольных точек; данная технология работает при любом числе контрольных точек.
Вышеизложенный алгоритм генерирования кривой может быть легко реализован в подпрограмме
Point2 curvePt(double t. Real PolntArray pts)Подпрограмма возвращает точку V(t) для каждого вводимого в нее значения t. Этот алгоритм будет более подробно рассмотрен в тематическом задании 11.4.
Пример 11.6.1. Расширение метода для рисования замкнутых кривых
Нетрудно расширить вышеизложенную технологию так, чтобы с ее помощью можно было генерировать замкнутые кривые, подобные изображенной на рис. 11.26, а. На рис. 11.26, б показан замкнутый вариант кривой, изображенной на рис. 11.25. При этом к уравнению (11.52) нужно только добавить два слагаемых и две контрольные точки, дублирующие точки Рй и Р{. (Тогда Р7 = Р0 и Ps = Рг) Мы знаем, что при t = 7 предыдущая кривая проходила через середину участка Р5Р6. Тогда при t = 8 кривая пройдет через середину отрезка Р6РГ а при t - 9 через середину отрезка Р7РВ, замыкая кривую. В упражнениях приводится также альтернативный метод.
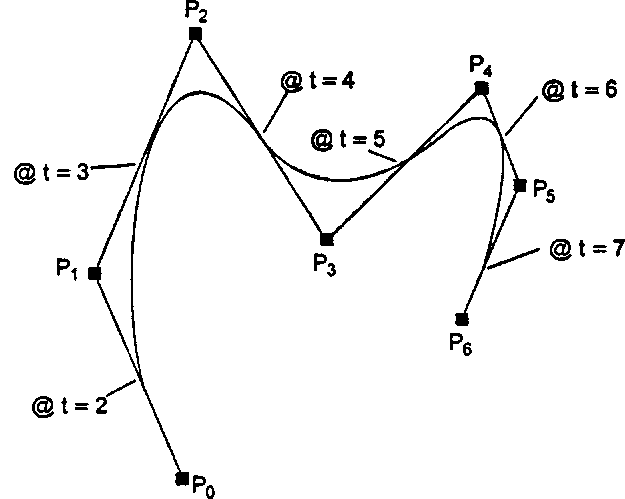
Рис. 11.25. Проектирование кривой с использованием смещений функций д(.)
11.6. Нахождение лучших стыковочных функций
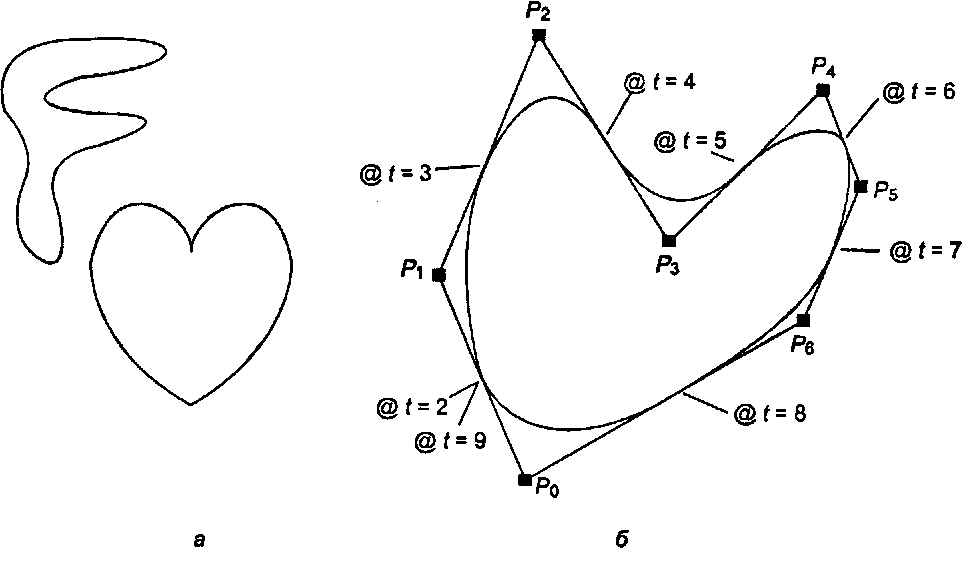
Рис. 11.26. Генерирование замкнутых кривых
Практические упражнения
11.6.1. Существует ли стыковочная функция, являющаяся полиномом четвертого Рассмотрим полином четвертой степени г(г) - atf + bl? + ct1 + dt + е. Существуют ли такие значения коэффициентов а, Ъ, с, d, е, при которых эта функция проходит через нулевую точку, а ее первая производная равна нулю при с - 0 и при с - 1? Если да, то найдите соответствующие значения и нарисуйте кривую.
