Практическое упражнение
9.7.1. Какие из этих точек лежат внутри К -1?
Пусть с = -1. Какие из нижеперечисленных стартовых точек лежат внутри плотного множества Жюлиа? О s = -0,5, О s = ±l, О s = ±2, О 5-±1,5.
Обобщая, можно сказать, что если орбита начинается достаточно близко от неподвижной точки притяжения, то орбита «всасывается» в эту точку. Если Же орбита начинается слишком далеко, то она взрывается. Множество тех точек, которые «всасываются», образуют так называемый бассейн притяжения (basin of attraction) неподвижной точки р. Это множество в точности совпадает с плотным множеством Жюлиа Кс. Нетрудно показать, что неподвижная точка, лежащая внутри круга \г\ = 1/2 (с центром в начале координат и с радиусом 1/2), является точкой притяжения.
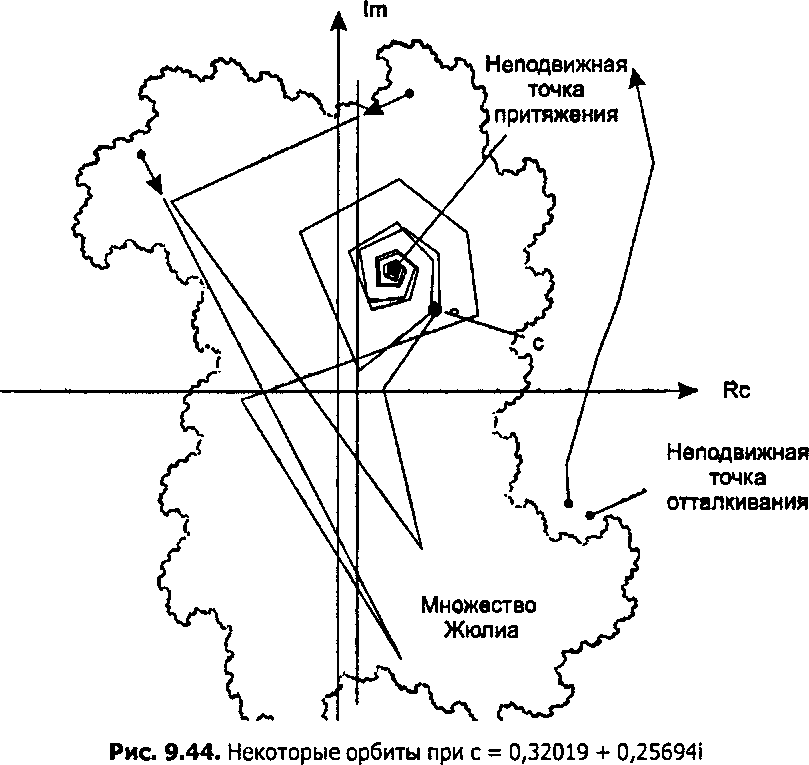
На рис. 9.44 схематически изображено множество Жюлиа при с = 0,32019 + 0,25694г. (Для простоты на рисунке проведена только граница множества Кс.) Кроме того, на рисунке показаны заданное значение с и две неподвижные точки (0,18681 + 0,4102 li и 0,81319 - 0,41021*'). Все точки, находящиеся вне/С, имеют взрывающиеся орбиты; на рисунке показан пример такой орбиты. Все точки внутри Кс имеют орбиты, которые прямо или по спирали втягиваются неподвижной точкой притяжения; два примера таких орбит также приведены на рисунке.
Отметим, что если стартовая точка лежит внутри множества Кс, то все точки ее орбиты также должны лежать внутри Кс, поскольку они сами являются полноправными стартовыми точками и все они образуют конечную орбиту. Также отметим, что неподвижная точка отталкивания находится на границе множества Кс. Это имеет место всегда.
Приближение к бесконечности
Множество Кс для двух простых случаев Оказывается, что при двух значениях с множество Кс имеет простой вид (но только для этих случаев).
1. с = 0: при старте из произвольной точки s орбита равна s, s2, s4,sn.....поэтому орбита всасывается по спирали в 0 при |s| < 1 и взрывается при \s\ > 1. Следовательно, К0 является множеством всех комплексных чисел, лежащих внутри единичного круга (unit circle), а именно круга с радиусом 1 с центром в начале координат. (Где в этом случае находятся две неподвижные точки?)
