1. Произвольный треугольник.
2. Любой гексагон, имеющий центр симметрии.
3. Любой четырехугольник.
Давайте продемонстрируем эти утверждения одно за другим.
1. Чтобы показать, что любой треугольник заполняет плоскость, повернем его вокруг середины одной из его сторон, чтобы образовать параллелограмм, который заполняет плоскость.
2. Если гексагон имеет центр симметрии (то есть если гексагон не изменяется при повороте его вокруг центра на 180°), тогда его противоположные стороны параллельны и равны по длине. Как показано на рис. 9.15, а, такие гексагоны всегда «прилегают» друг к другу без зазоров после соответствующего переноса.
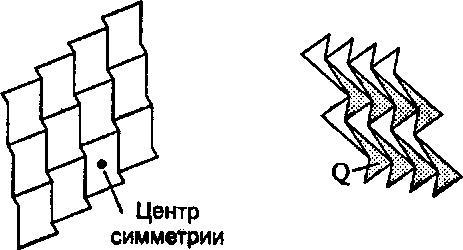
в б Рис. 9.15. Любой центрально-симметричный гексагон заполняет плоскость
3. Наконец, из любого четырехугольника можно построить гексагон с точкой симметрии, просто поворачивая четырехугольник вокруг середины одной из его сторон, как показано на рис. 9.15, б. Поскольку такой гексагон заполняет плоскость, то и любой четырехугольник - тоже!
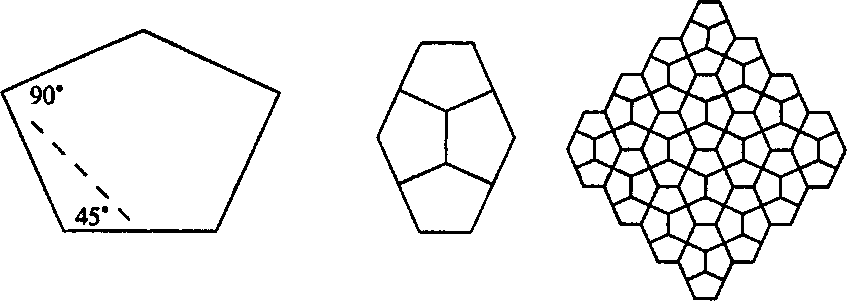
в б в Рис. 9.16. Каирская мозаика Произвольный 5-угольник не может заполнить плоскость, однако один вид неправильного равностороннего пентагона (пятиугольника) может, как это показано на рис. 9.16. Пентагон на рис. 9.16, а
Приближение к бесконечности
имеет равные стороны, однако его внутренние углы не равны. Четыре таких Пентагона, составленные вместе, образуют гексагон, который заполняет плоскость. Это носит название Каирской мозаики (Cairo tiling), поскольку многие улицы столицы Египта Каира вымощены именно таким узором.
Некоторые другие полигоны, которые могут или, напротив, не могут заполнить плоскость, показаны на рис. 9.17. На рис. 9.17, а приведены некоторые из знаменитых полимино (polyominoes) Соломона Голомба (Solomon Golomb - [Golomb, 87]), образованные соединением единичных квадратов «ребро к ребру». Полимино являются обобщением домино, которые состоят только из двух квадратов, соединенных ребром к ребру. Полиамонды (polyiamonds) образованы посредством соединения конгруэнтных равносторонних треугольников [Gardner, 78]; несколько примеров приведены на рис. 9.17, б. В упражнении 9.4.1 предлагается определить, какие из изображенных на рисунке полигонов заполняют плоскость.
