Чтобы понять смысл формулы (7.16), используем обычную камеру. Мы будем работать в системе координат камеры, тогда вектор п - (0,0,1). Проецировать будем на плоскость ху, для которой точка В = (0, 0, 0). (Это немного проще, чем проецирование на ближнюю плоскость.) Тогда
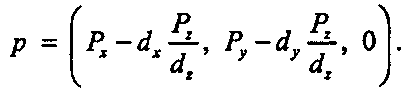
(Проверьте эту формулу!) Параллельные проекции подразделяются на два основных типа, как показано на рис. 7.41.
1. Косоугольная: направление проекции d не параллельно вектору п.
2. Ортографическая: направление проекции d параллельно вектору п.
7.6. Классификация проекций
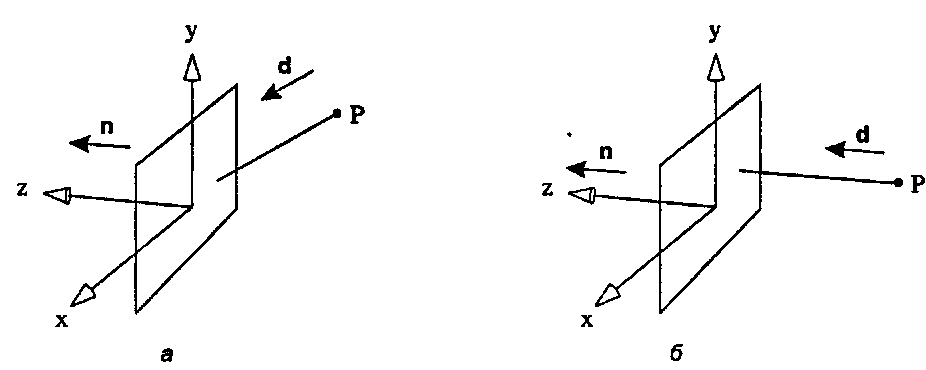
Рис. 7.41. Параллельные проекции при работе в системе координат камеры: а) общий случаи направления d; б) d параллельно п На рис. 7.41, я показан общий случай направления вектора d, не обязательно параллельного вектору п. (Разумеется, мы не будем выбирать его так, чтобы dz было равно нулю.) Рисунок 7.41, б демонстрирует случай, когда векторы d и п параллельны, так что dx и dy равны нулю. Рассмотрим каждый из этих типов поочередно.
Ортографические проекции При ортографических проекциях два компонента dx и dy равны нулю. Тогда точка р становится равной р = (Рх, Р, 0). Таким образом, ортографическое проецирование сводится к простому отбрасыванию третьего компонента точки Р в координатах камеры.
Интересно посмотреть, как OpenGL выполняет ортографическую проекцию. Напомним, что OpenGL для описания отображаемого объема камеры использует проекционную матрицу. Проекционная матрица, в частности, определяет, как преобразовывать вершины, чтобы «втиснуть» их в канонический отображаемый объем (CVV). Пусть фактический отображаемый объем простирается от / до г (сокращения от left - левый и right - правый) по оси х, от Ъ до t (bottom - нижний и top - верхний) по оси у, от -я до -/ (near - ближний и far - дальний) по оси z. Для преобразования параллелепипеда, сформированного таким образом внутри CW, мы должны произвести перемещение и масштабирование так, чтобы CW простирался от -1 до 1 в каждом измерении. Легко убедиться (см. упражнения), что матрица
