7.6.3. Вычисление точек схода Найдите положения двух точек схода на рис. 7.36, а для произвольного значения угла 9.
7.6.4. Создание двухточечных перспективных проекций Приведите три примера сочетания eye и 1 оок для камеры, создающей интересные двухточечные перспективные проекции единичного куба Для каждого примера вычислите фактические положения точек схода.
Трехмерный просмотр
7.6.2. Параллельные проекции Ниже исследуются различные типы параллельных проекций. В главе 5 мы ввели понятие параллельных проекций в качестве простого способа просмотра объектов. Для задания отображаемого объема была использована функция gWrthoO, a OpenGL делал все остальное. Теперь мы взглянем несколько пристальнее на природу параллельной проекции и разграничим ее различные типы, используемые на практике.
Известно, что в случае перспективной проекции все точки Р сцены проецируются на плоскость просмотра с помощью проецирующих лучей (projectors), сходящихся в точке глаза: каждый проецирующий луч определяется точкой Р и глазом, и все эти лучи имеют различные направления. Для параллельных проекций, напротив, все проецирующие лучи имеют одно и то же направление, назовем его d. На рис. 7.40 показано проецирование двух произвольных точек: точка Р проецируется в р на плоскости просмотра, а точка Q-ъд, причем обе точки - в направлении вектора d.
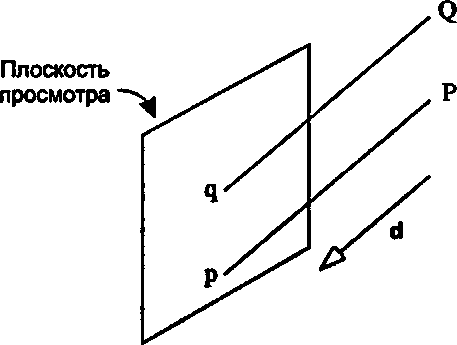
Рис. 7.40. Параллельные проекции Немного теории касательно параллельных проекций В какую точку р проецируется точка Р? Рассмотрим плоскость с нормалью п, проходящую через некоторую точку В. Тогда точка р расположена в этой плоскости в месте пересечения плоскости и луча, исходящего из точки Р по направлению А Ранее мы уже неоднократно производили такое вычисление. Если параметрическая форма этого луча Р + то мы подставляем это выражение вместо <2 в уравнение плоскости п ((2 - В) = 0 и решаем его относительно £. Для получения точки соударения подставляем это значение Ь в выражение Р + др.
р=Р+й!^(^. (7.1б)
п-<1
Это выражение сильно отличается от того, которое мы использовали при перспективной проекции. В частности, здесь отсутствует уменьшение расстояния; это означает, что в знаменателе отсутствует член, зависящий от Р. (Отметим вдобавок, что замена направления <1 на на -6 не окажет никакого влияния на результирующую проекцию.)
