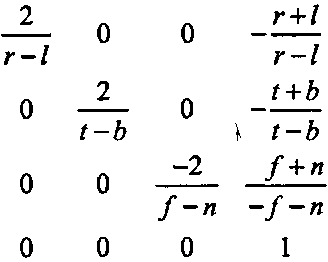
(7.18)(проекционная матрица OpenGL для ортографической проекции) действительно преобразует отображаемый объем в CVV. Такая матрица формируется функцией glOrthoO. Если на нее умножить точку Р (выраженную в однородных координатах), то получим именно ту точку р, которую предоставляет OpenGL для отсечения и отображения в порт просмотра. Отметим, что OpenGL не устанавливает z-компонент в нуль, как это делали мы; он производит преобразование, а не проецирование. В конце операции он все-таки осуществляет проецирование, отделяя z-компонент; компоненты х и у в экранных координатах используются при рисовании, а компонент z - для оценки глубины.
Типы ортографических проекций Существуют различные типы ортографических проекций, отличающихся друг от друга ориентацией камеры в мировой системе координат. Эти проекции названы в соответствии с тем, как расположено относительно мировых координатных осей направление камеры п.
Трехмерный просмотр
Многовидовые ортографические проекции. Они представляют традиционные виды объекта сверху, спереди и сбоку. Вектор п поочередно устанавливается параллельным векторам к, 1,}, и интересующий нас объект рисуется в каждом случае. На рис. 7.42 показан пример таких проекций. Многовидовые ортографические проекции специально приспособлены для технического черчения, так как размеры объекта можно определить непосредственно, особенно если он «кубовидный» и различные его грани выровнены относительно мировых осей.
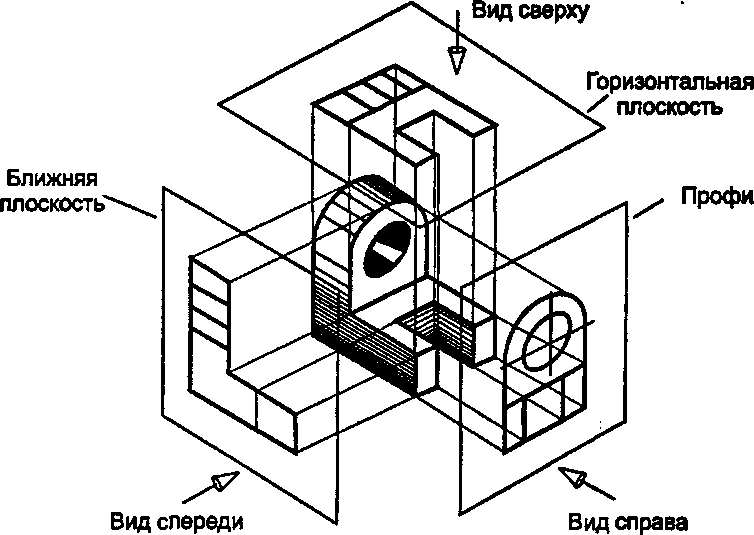
Рис. 7.42. Многовидовое ортографическое черчение Аксонометрические проекции. В аксонометрических проекциях вектор п выбирается так, чтобы наилучшим образом передать трехмерную «суть» формы объекта При такой проекции вектор п обычно не параллелен ни одной из главных осей; скорее, он ориентируется так, чтобы были видны три смежные грани (кубовидного) объекта. Выбор тех граней, которые делаются видимыми, зависит от того, какие грани объекта важны и должны быть выделены особо. Кроме того, одна из главных осей обычно делается вертикальной. Параллельные прямые такого объекта, разумеется, и видны как параллельные, однако если прямая удаляется от наблюдателя, то она укорачивается с некоторым коэффициентом. На рисунке 7.43 показан случай, когда вектор п составляет угол ос с осью х.
