Интересно посмотреть, что получится, если мы будем рассматривать в двухточечной перспективе сцену с бесконечной сеткой, с которой мы впервые встречались на рис. 7.21. На рис. 7.37 показан случай, когда глаз по-прежнему находится в у - 1 и смотрит горизонтально, однако камера повернута влево, так что п = (0,74,0,0,67). Теперь обе совокупности прямых сходятся к горизонту, образуя две далеко отстоящие точки схода. (Каковы численные значения этих точек схода?) Многие из наиболее удаленных прямых на рисунке не показаны, так как они становятся настолько близкими одна к другой, что их невозможно различить.
Трехмерный просмотр
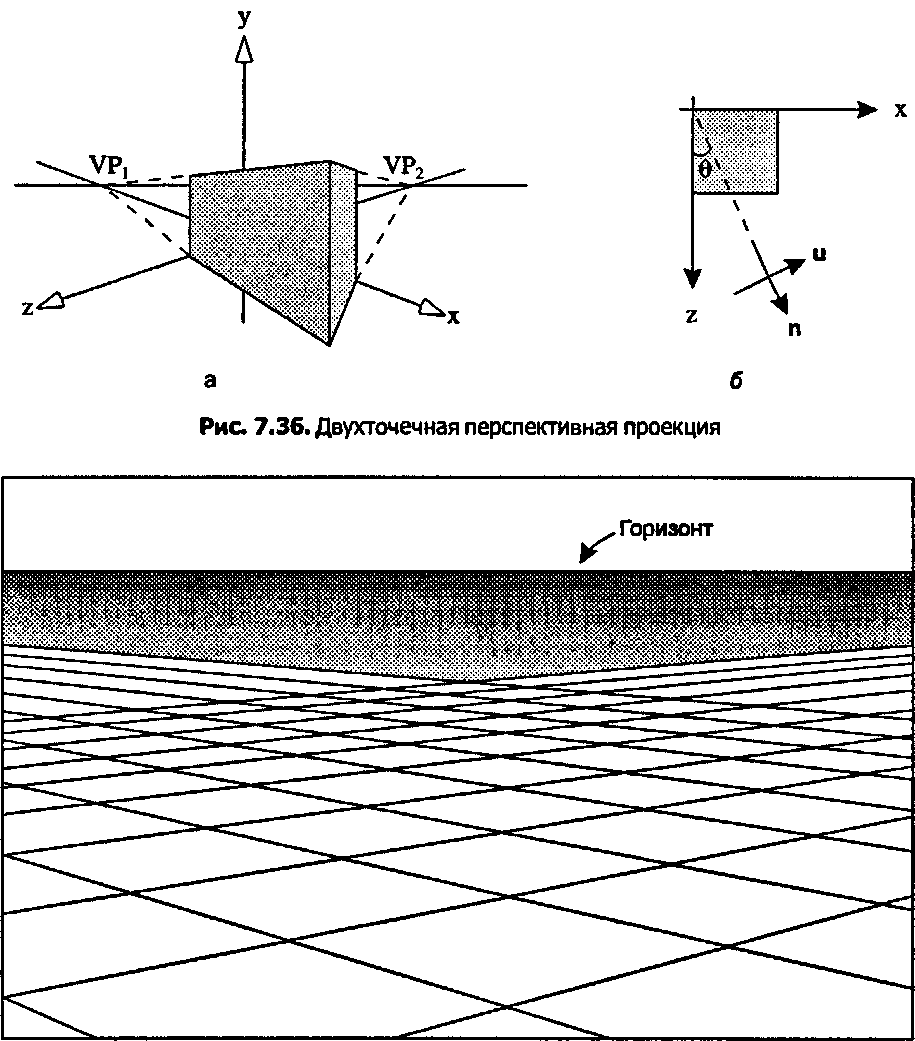
Рис. 7.37. Бесконечная сетка в двухточечной перспективе Трехточечная перспективная проекция При трехточечной перспективной проекции все три главных оси имеют конечные точки схода и все три оси пересекают плоскость просмотра. Вектор п не перпендикулярен ни одной из осей, так что все его компоненты - ненулевые.
На рис. 7.38 показан куб в трехточечной перспективной проекции. Видны все три конечные точки схода.
Художники часто используют точки схода при рисовании перспективы, с целью выделить определенные свойства или усилить впечатление от рисунка. Блестящая литография М К. Эшера (М. С. Escher) на рис. 7.39 передает ощущение пространства, полученное с помощью трехточечной перспективы. (Где на этом рисунке расположены три точки схода?)
Практические упражнения
7.6.1. Задание одноточечной перспективной проекции Для установки нужной камеры мы выбираем в приложении eye и look, а вектор п определяется как разность eye - look. Дайте три примера сочетания eye и look, которые дадут интересные одноточечные проекции единичного куба.
7.6. Классификация проекций
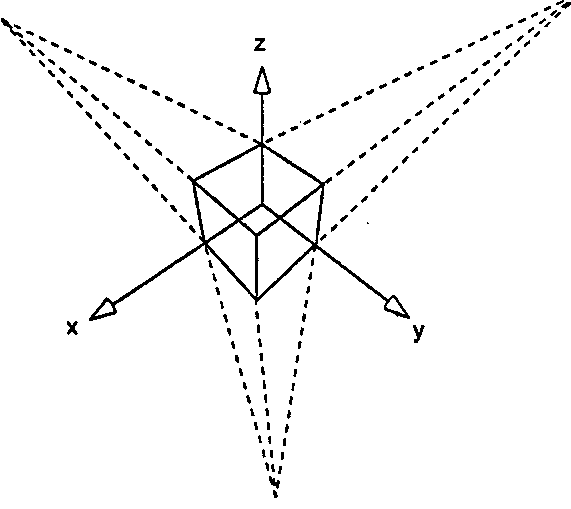
Рис. 7.38. Трехточечная перспективная проекция

Рис. 7.39. Работа М. К. Эшера «Восхождение и спуск»: трехточечная перспективная проекция (© 1988 М. С. Вспег Не^/Согооп АЛ-Ваагп-НоНапа'. Использовано с разрешения)
7.6.2. Положение точки схода Нарисуйте от руки единичный куб и мировые координатные оси в одноточечной перспективной проекции для камеры с eye = (2,3,4).
