Особый интерес вызывает то, как перспективное преобразование преобразует отображаемый объем камеры, поскольку если мы собираемся производить отсечение в деформированном пространстве, то мы будем отсекать границами деформированного отображаемого объема. Преобразование блестяще справляется с этой проблемой: форма деформированного отображаемого объема прекрасно подходит для простого и эффективного отсечения! На рис. 7.25 показано, как преобразуются отображаемый объем и другие формы. Ближняя плоскость W, имеющая уравнение z -N, отображается в плоскость W, заданную уравнением z = -1, а дальняя плоскость отображается в плоскость z ** +1. Верхняя стенка Т «разворачивается» в горизонтальную плоскость 7", так что последняя становится параллельной оси z. Нижняя стенка S становится горизонтальной плоскостью S', а две боковые стенки становятся также параллельными оси z. Таким образом, отображаемый объем камеры преобразуется в параллелепипед!
Трехмерный просмотр
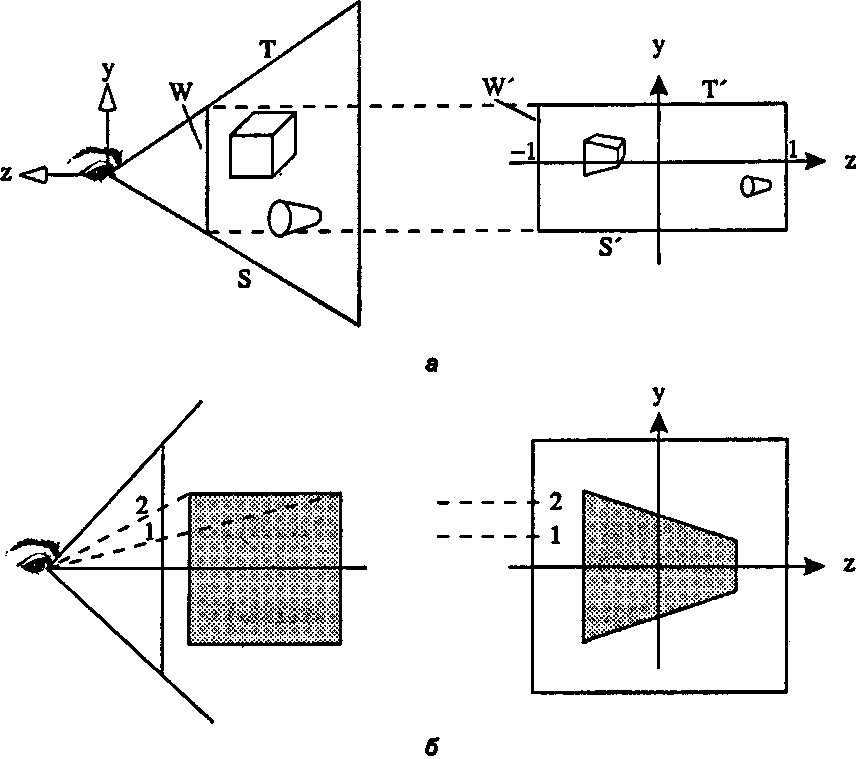
Рис. 7.25. Деформирование отображаемого объема перспективным преобразованием Легко доказать, что все эти плоскости преобразуются именно таким образом, поскольку все входящие в них прямые линии либо параллельны ближней плоскости, либо проходят через глаз. Внимательно проверьте следующие утверждения.
Утверждение. Прямые, проходящие через глаз, преобразуются в прямые, параллельные оси г.
Доказательство. Все точки прямой, проходящей через глаз, проецируются в одну и ту же точку, например (**, у*) на плоскости просмотра. Тогда все точки, принадлежащие этой прямой, преобразуются во все точки (х, у, г), тд,ех-х*,у - у*, а г принимает все значения псевдоглубины между -1 и 1.
Утверждение. Прямые, перпендикулярные оси г, преобразуются в прямые, перпендикулярные оси г.
Доказательство. Все точки этой прямой имеют одну и ту же координату г, поэтому все они преобразуются в точки с одним и тем же значением псевдоглубины.
Используя эти утверждения, нетрудно вывести точную форму и размеры деформированного отображаемого объема.
