Следовательно, перспективное преобразование переносит трехмерную точку Р в другую трехмерную точку Р' в соответствии с отображением

Когда вступает в игру эта проекция? Далее по конвейеру первые два компонента этой точки используются при рисовании, чтобы отметить в экранных координатах положение изображаемой точки. Третий компонент «отщепляется» для будущей проверки глубины. Пока нас интересует только положение точки на экране, игнорирование третьего компонента эквивалентно замене его на нуль, то есть
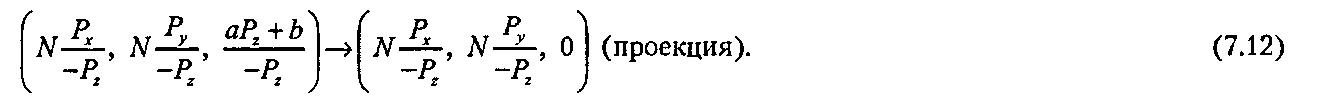
Это как раз то, что мы делали в главе 5 при ортографическом проецировании точки (перпендикулярно к плоскости просмотра), когда устанавливали камеру в наших первых опытах просмотра трехмерной сцены. Все подробности ортографических проекций мы будем изучать позднее. На данный момент можно сделать следующий вывод:
(перспективная проекция) = (перспективное преобразование) + + (ортографическое преобразование).
Такое разложение перспективной проекции на частное преобразование, за которым следует (тривиальная) проекция, будет весьма плодотворным как для написания алгоритмов, так и для лучшего понимания того, что конкретно происходит с каждой точкой по мере ее прохождения через графический конвейер. В OpenGL этап преобразования отделен от этапа проецирования; фактически он включает в себя отсечение, перспективное деление и одно дополнительное преобразование между ними. Теперь рассмотрим более подробно часть процесса, относящуюся к преобразованию.
Геометрическая природа перспективного преобразования Перспективное преобразование превращает трехмерную точку Р в другую трехмерную точку в соответствии с уравнением (7.11), чтобы «подготовить» эту точку к проецированию. Полезно трактовать это преобразование как «деформирование» трехмерного пространства и посмотреть, как оно переводит одну форму в другую. Очень важно, что при этом преобразовании сохраняются прямолинейность и плоскостность, так что прямые линии преобразуются в прямые линии, плоскости - в плоскости, а полигональные грани - в другие полигональные грани. Кроме того, сохраняется и «промежуточность» («in-between-ness»), так что если точка находится внутри объекта, то преобразованная точка будет также находиться внутри преобразованного объекта. (Наш выбор функции псевдоглубины был обусловлен необходимостью сохранить эти свойства, что будет доказано в упражнениях.)
