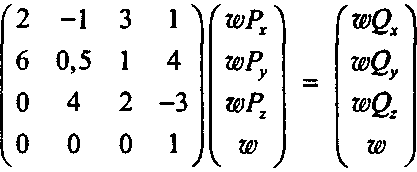
то последний компонент (2 никогда не изменится и будет всегда равен хю. Следовательно, можно преобразовать (2 обратно в обычные координаты обычным способом.
Однако произойдет нечто новое, если четвертая строка будет отличаться от значения (0,0,0,1). Рассмотрим важный пример: г N 0 0 0)

Четвертая строка этой матрицы равна (0,0, -1,0) для любых значений Ы, а, Ь. Это похоже на то, что позднее мы назовем «проекционной матрицей». Если мы умножим эту матрицу на точку, выраженную в однородных координатах с любым значением хю, то есть:
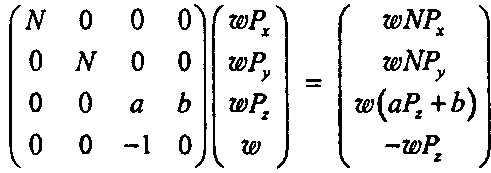
то получим обычную точку. Но какую именно? Чтобы выяснить это, разделим все на четвертый компонент и отбросим ее. Тогда получим
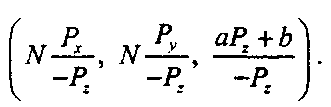
Это именно то, что нам нужно, согласно формуле (7.7). Таким образом, однородные координаты позволяют нам создавать перспективу при помощи умножения матриц! Однако для достижения такого результата мы должны всегда делить все компоненты на четвертый компонент. Этот этап называется перспективным делением (perspective division).
Матрица, четвертая строка которой не равна (0, 0, 0, 1), производит неаффинное преобразование. Вместо этого она выполняет преобразование более общего класса, называемое перспективным преобразованием (perspective transformation). Отметим, что это именно преобразование, а не проекция; ведь проекция уменьшает размерность точки до упорядоченной тройки или пары, в то время как перспективное преобразование принимает четверку и возвращает тоже четверку.
Рассмотрим алгебраический смысл внесения ненулевых величин (А, В, С, D) в четвертую строку матрицы. Когда мы умножаем матрицу на (Pz, Р, Рг, 1) (или на что-нибудь в этом роде), четвертый член получающейся в результате точки приобретает вид APz + ВРу + СР2 + D, то есть линейно зависит от каждого компонента точки Р. После перспективного деления этот член появляется в знаменателе этой точки. Именно такой знаменатель необходим для получения геометрического эффекта перспективной проекции на главной плоскости, что мы покажем в упражнениях.
7.4. Перспективные проекции трехмерных объектов
