Нарисуйте, как будет выглядеть поверхность, образованная вращением фигуры Лиссажу из равенства (6.19) вокруг оси у при М = 2, N = 3, ф = 0.
6.5.22. Вращение п-угольников Нарисуйте поверхность, образующуюся при вращении квадрата с вершинами (1,0,0), (0,1, 0), (-1, 0, 0), (0,-1, 0) вокруг оси у. Выполните аналогичную процедуру для Пентагона и гексагона.
Dengo отзывы о программе лояльности.
Важное семейство поверхностей - поверхности второго порядка, или квадрики - являются трехмерными аналогами конических сечений, или коник (эллипса, параболы и гиперболы, которые мы рассматривали в главе 3). Некоторые из поверхностей второго порядка обладают красивой формой и могут найти широкое применение в графике.
На рис. 6.61 приведено шесть поверхностей второго порядка. Нам требуется охарактеризовать только «базовые» варианты этих форм, ибо все интересующие нас изменения можно получить посредством масштабирования, поворота и смещения соответствующих обобщенных форм. Известно, например, что внешне-внутренняя функция для эллипсоида имеет вид: причем данный эллипсоид располагается: по х от -а до я, по у от -Ъ до Ь, по г от -с до с. Эта поверхность может быть получена из формулы базовой сферы путем ее масштабирования вдоль осей х, у, г соответственно с множителями а, Ъ, с, как мы уже вкратце описывали. Аналогично могут быть получены повернутые варианты эллипсоида.
Таблица 6.8 описывает шесть базовых квадрик, задавая и неявную, и параметрическую форму каждой из них. Позднее мы рассмотрим некоторые любопытные свойства каждой из этих поверхностей.
Легко убедиться, что каждая из этих параметрических форм согласуется с соответствующей неявной формой: достаточно просто подставить параметрические выражения в компоненты по х, у и г, после чего с помощью тригонометрических тождеств убедиться в том, что получается нуль.
6.5.8. Поверхности второго порядка
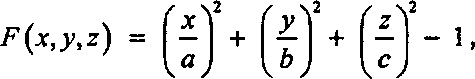
(6.43)6.5. Каркасные аппроксимации гладких объектов
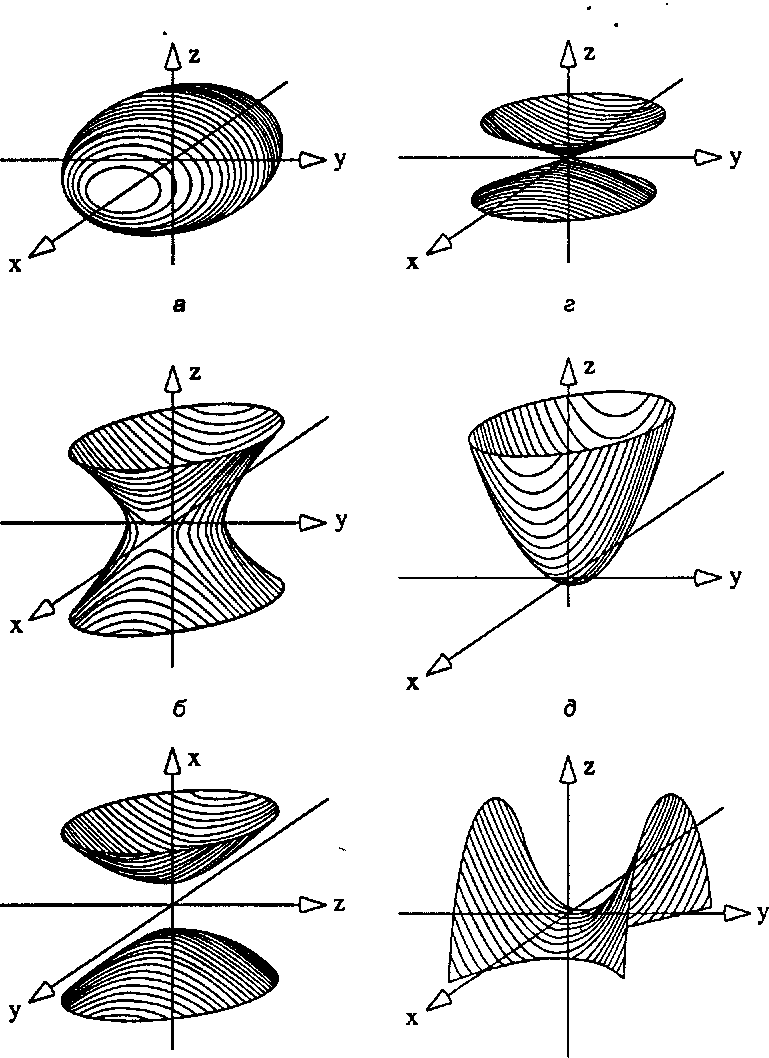
в е Рис. 6.61. Шесть поверхностей второго порядка: а) эллипсоид; 6) однополостный гиперболоид; в) двуполостный гиперболоид; г) эллиптический конус; д) эллиптический параболоид; ё) гиперболический параболоид
