Для того чтобы построить поверхность вращения в случае профиля, заданного дискретными точками, будем определять ij-ю вершину из равенства (6.40) в слегка измененной форме: РГ (X.cos(Mj),X.sin(Mi),2;.).
Практические упражнения
6.5.17. Базовые формы как поверхности вращения Опишите в параметрической форме профили для базовых сферы, цилиндра и конуса, а затем выразите их как поверхности вращения.
6.5.18. Вращение вокруг других осей Рассмотрим профильную кривую C(v) = (X(v), Z(v)), лежащую в плоскости xz, и произвольную ось, проходящую через начало координат и заданную единичным вектором г. Из уравнения (5.33) мы знаем, что матрица #.(9) осуществляет поворот точки на 9 радиан вокруг оси г: а) покажите, что поверхность вращения, полученная посредством развертки кривой С(р) вокруг оси г, имеет вид:
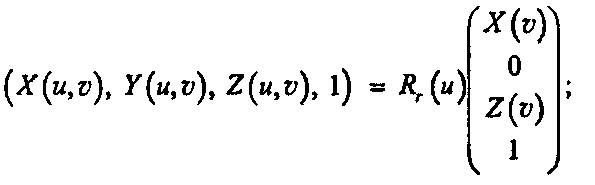
Глава б. Моделирование поверхностей полигональными сетками б) проверьте это равенство для частного случая вращения вокруг оси г; в) повторите пункт б) для вращений вокруг оси х и вокруг оси у.
6.5.19. Нахождение нормальных векторов Примените равенство (6.40) к равенству (6.25) для вывода формулы нормали к поверхности вращения в равенстве (6.41).
мониторинг давления в шинах грузовика.
Используйте результат пункта а) для нахождения нормалей к базовым сфере, цилиндру и конусу, после чего покажите, что эти результаты согласуются с полученными в разделе «Три „базовые" формы: сфера, цилиндр и конус». Докажите, что нормальный вектор к тору имеет вид: п(и, ю) = (соз(а) соз(и), соэ(&) зт(и), зт(»)) ф + Лсоб(&)).
Кроме того, найдите для тора внешне-внутреннюю функцию и вычислите нормаль с использованием градиента этой функции.
6.5.20. Эллиптический тор
Найдите параметрическое представление для следующих двух поверхностей вращения: О поверхность, которая получается, когда эллипс вида (асоъ(ю), Ъът(ю)) сначала смещается на К единиц вдоль оси х, а затем поворачивается вокруг оси у; О поверхность, которая получается, когда тот же самый эллипс поворачивается вокруг оси х.
6.5.21. «Фигура вращения Лиссажу»
