С(0 - ((а + bcos(qi))cos(pt), (а + bcos(qt))sin(pt), csin(qt)) (6.18)
для определенных значений констант а, Ь, с, р, q. На рис. 6.40, а параметры р и q равны соответственно 2 и 5, а на рисунке 6.40, б они равны 1 и 7.
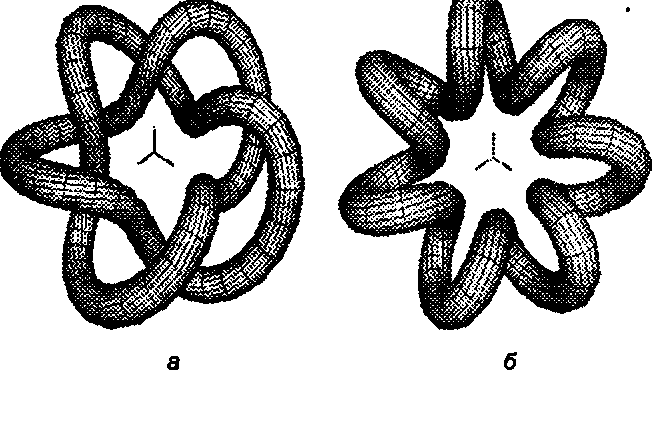
Рис. 6.40. Трубы на базе тороидальных спиралей На рис. 6.41 показана «морская раковина», полученная «надеванием» на спираль трубы с возрастающим радиусом. Для этого матрица из равенства (6.12) была умножена на матрицу масштабирования.
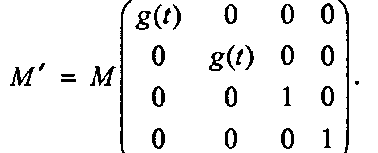
Масштабные множители в матрице зависят от £. Здесь принято £(г) = £. Можно также добавить к матрице поворот, и тогда труба будет закручиваться еще сильнее, если смотреть вдоль ее хребта.
Моделирование поверхностей полигональными сетками

Рис. 6.41. «Морская раковина» Одна из сложностей, связанных с использованием базисов Френе для прохождения кривых, заключается в том, что локальный базис иногда закручивается так, что на поверхности появляются нежелательные «узелки». В последних исследованиях, таких как работа Вонга [Wang, 206], найдены альтернативы базису Френе, которые создают менее закручивающиеся и, следовательно, более изящные поверхности.
Практические упражнения
6.4.4. Что такое N(t)?
Покажите, что вектор N(r) параллелен вектору С (г) - (c(f) С (r))C(f)/|c (t )|2 и поэтому указывает в направлении ускорения, если скорость и ускорение в точке г перпендикулярны.
6.4.5. Базис для винтовой линии Рассмотрим круговую спираль, упоминавшуюся в тексте. Докажите правильность формул для единичных векторов касательной, нормали и бинормали. Покажите также, что эти векторы имеют единичную длину и взаимно перпендикулярны. Мысленно представьте себе, как ориентируется локальная система координат по мере продвижения вдоль кривой.
На рис. 6.42 приведено еще два примера. На рис. 6.42, а показан гексагон, скользящий вдоль эллиптического хребта и образующий своего рода эллиптический тор, а на рис. 6.42, б - составленная из частей обернутая семиугольником фигура Лиссажу (Увва^ив), которая описывается формулой
