Моделирование поверхностей полигональными сетками
будет использоваться в качестве оси системы координат, нормируем его и получим «единичный вектор бинормали» («unit binormal vector»): С(0 х C(t)
В(0 = (6.14)
\C(t) х С(0
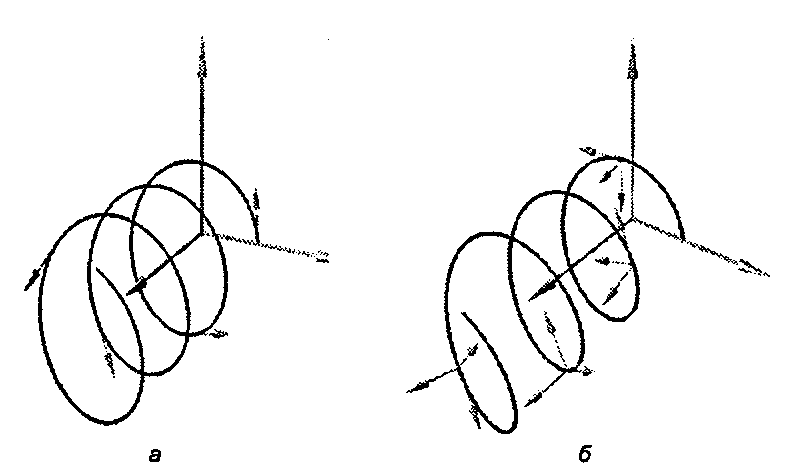
Рис. 6.38. Касательные к спирали (а); показан базис Френе при различных значениях t вдоль спирали (б)
Затем с помощью нового векторного произведения получим вектор, перпендикулярный к векторам T(t) и B(t)"images/tmp8E4A-398.png">
(6.16)Численное определение базиса Френе Если формула кривой C(t) сложна, то вычисление ее последовательных производных в аналитической форме (чтобы формулы для векторов Т(0, В(£) и N(t) могли быть «зашиты» в программу) может оказаться затруднительным. В качестве альтернативы возможна численная аппроксимация этих производных по формулам:
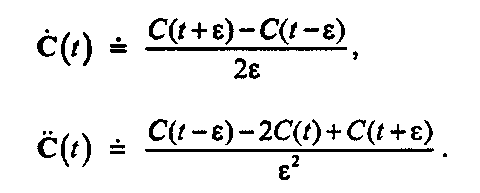
(6.17)Вычисление по этим формулам обычно дает приемлемые направления векторов Т(г), В(с) и N(c), хотя пользователю следует отдавать себе отчет в том, что численное дифференцирование - изначально неустойчивый процесс [Burden, 37].
На рис. 6.39 показан результат «нанизывания» десятиугольника на винтовую линию с использованием базиса Френе. Винтовая линия была построена по 30 замерам (фиксированным значениям
6.4. Экструзивные формы
параметра), в каждом из замеров был построен базис Френе, после чего десятиугольник строился в новом базисе.
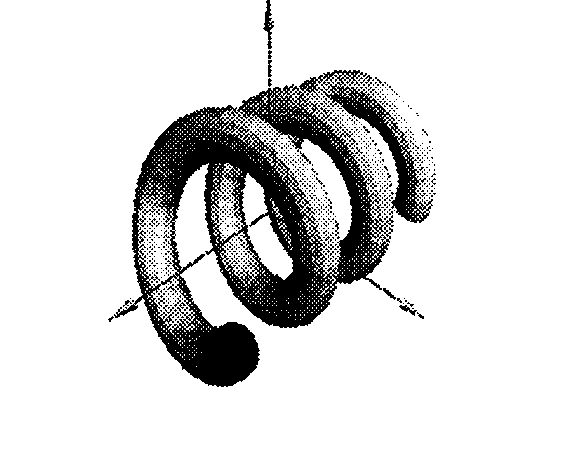
' Рис 6.39. Труба, нанизанная на винтовую линию
*На рис. 6.40 представлены два других интересных примера, основанные на тороидальной спирали (впервые мы встречались с ней в разделе «Применение параметрического задания кривой») [Gray, 91]. Ребра отдельных граней нарисованы для наглядности, чтобы было видно, как поворачивается труба по мере своей протяженности. Рисование ребер ее сетки рассматривается в тематическом задании 6.7. Тороидальная спираль получается путем оборачивания линии вокруг тора. (Попробуйте вообразить не видимый на рисунке оборачиваемый тор.) Тороидальная спираль задается формулой:
