гдеМ= 2,^=3, 0 = 0.
В тематическом задании 6.5 рассматриваются дополнительные подробности построения сеток, моделирующих трубки на основе параметрически заданной кривой.
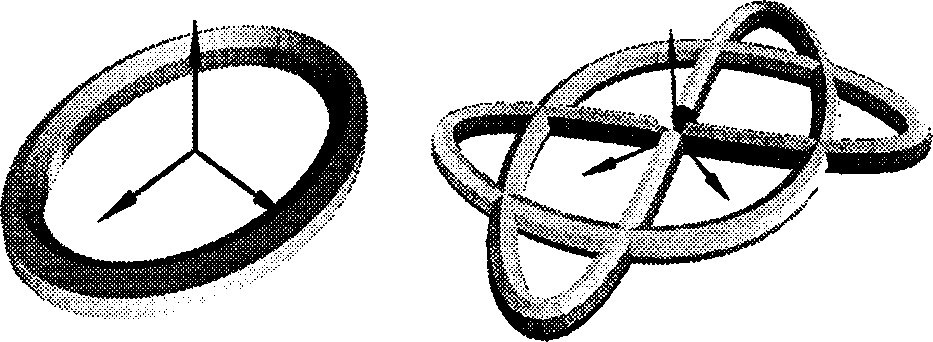
а б Рис. 6.42. Гексагон, нанизанный на эллипс и образующий эллиптический тор (а); гептагон (7-угольник), нанизанный на фигуру Лиссажу (б)
С(г) = (rcos(Mr + ф), 0, rsin(№)),
(6.19)6.4. Экструзивные формы
6.4.5. «Дискретно» заметаемые поверхности вращения Трубки, представленные в предыдущем разделе, для задания новой системы координат в каждой точке хребта используют аффинные преобразования. Если же мы применим в качестве аффинных преобразований чистые вращения и поместим все точки хребта в начало координат, то мы получим обширное семейство многогранных форм. На рис. 6.43 приведен пример, в котором полигон основания - теперь мы будем называть его профилем (profile) - имеет начальное положение в трех единицах по оси х и затем посредством последовательных шагов поворачивается вокруг оси у, так что получается аппроксимация (приближение) тора. Такая операция эквивалентна круговой развертке с заметанием (circularly sweeping) формы вокруг оси, а результирующую форму часто называют поверхностью вращения (surface of revolution). Стандартные поверхности вращения рассматриваются в разделе «Каркасные аппроксимации гладких объектов»; здесь же мы просто формируем их дискретное приближение, поскольку развертка осуществляется конечными шагами.
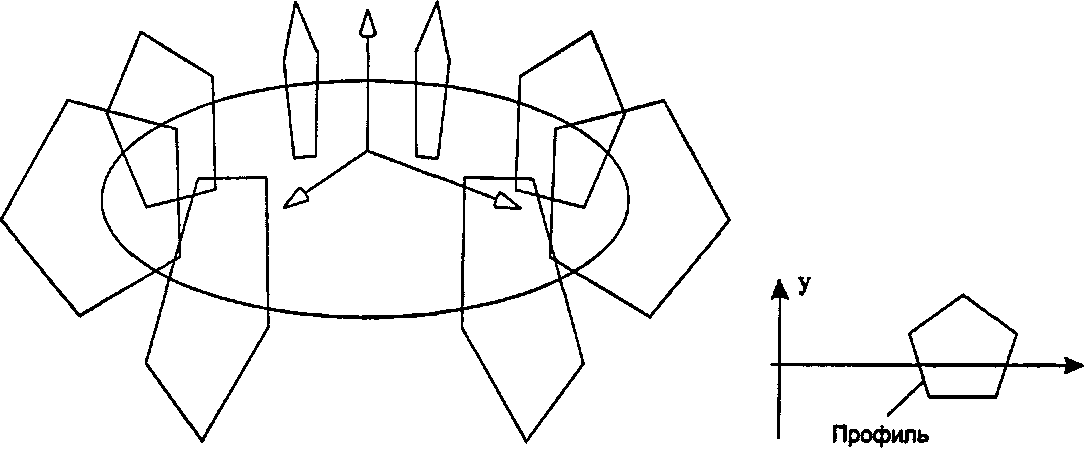
Рис. 6.43. Дискретные шаги заметания с вращением
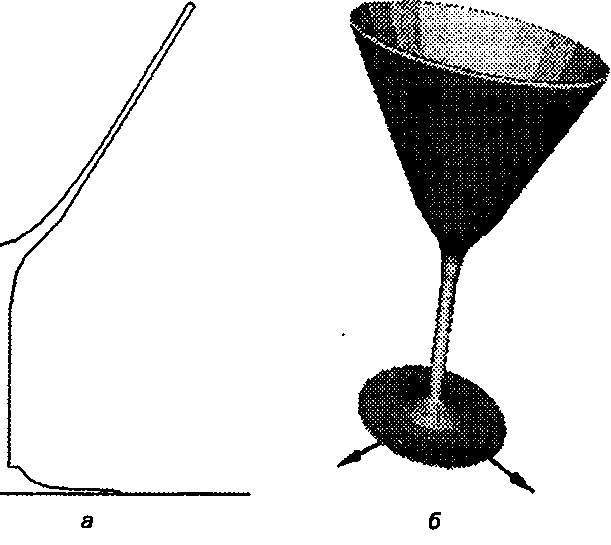
Рис. 6.44. Аппроксимация бокала для мартини с помощью дискретной развертки с заметанием ломаной линии: а) профиль; б) заметаемая поверхность
Рисунок 6.44 показывает пример создания изображения бокала для мартини. Профиль здесь является не замкнутым полигоном, а простой ломаной с вершинами Р;. = (х^ у./ 0). Если такую ломаную
13 Ф. Хилл
Моделирование поверхностей полигональными сетками
поместить под К равноотстоящих углами относительно оси у, то преобразования будут описываться матрицами:
0^о
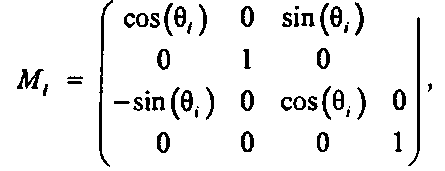
где угол б,. = 2т/К, г = 0,1,…, .К - 1. Отметим, что здесь отсутствует перемещение. Данное преобразование достаточно просто для того, чтобы мы смогли непосредственно выписать координаты вершин. Поворот устанавливает точки г'-й «перетяжки» ломаной в виде
