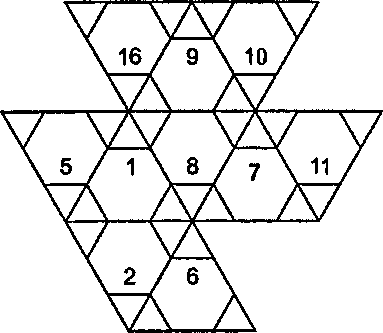
Рис. 6.27. Построение бакибола Геодезические купола Труднее всего примириться с хорошим примером.
Обнаружил интересный источник интересных новостей.
Марк Твен (Mark Twain)
Хотя Бакминстер был пионером во многих направлениях, более всего он знаменит введением понятия геодезических куполов [Fuller, 71]. Эти тела составляют интересный класс полиэдров, обладающих многими полезными свойствами. В частности, геодезический купол, созданный из реальных материалов, чрезвычайно прочен для своего веса.
Геодезический купол может принимать множество различных форм, но все они расположением своих граней, обычно треугольных, аппроксимируют сферу. Когда сфера аппроксимирована такими гранями, ее нижняя половина удаляется, и оставшаяся верхняя половина образует знакомую купольную форму. На рис. 6.28 показан пример, основанный на икосаэдре.
Для определения граней каждое ребро икосаэдра разбивается на 3FpaBHbix частей,- где величина F- введенная Фуллером частота (frequency) купола В данном примере F = 3, так что каждое ребро икосаэдра разделено на три части для образования девяти меньших треугольных граней (рис. 6.29, а).
Моделирование поверхностей полигональными сетками
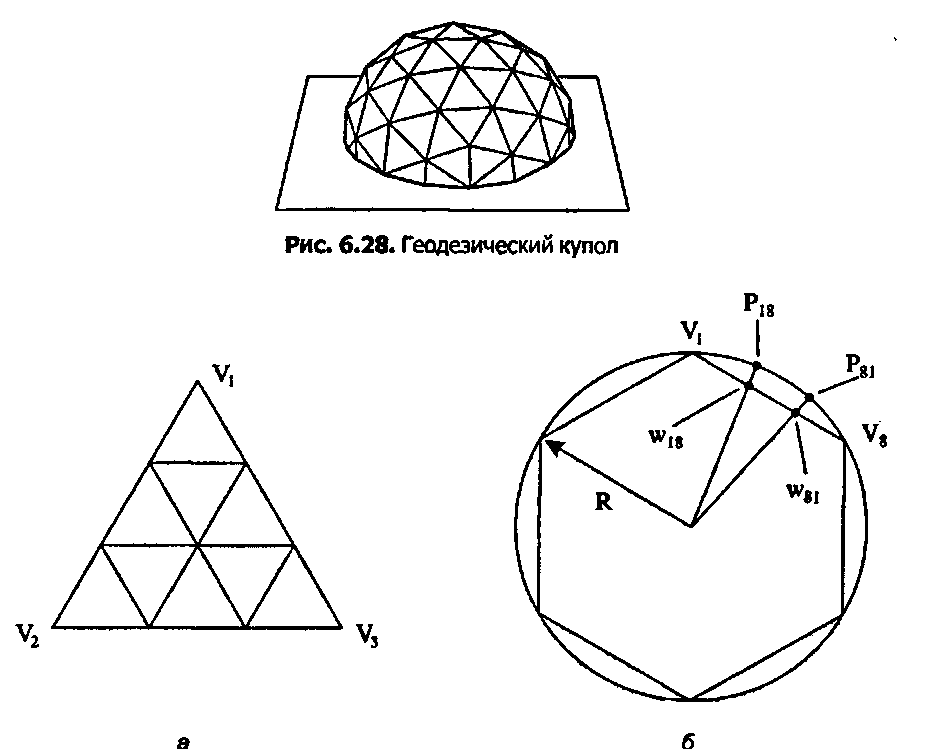
Рис. 6.29. Построение новых вершин для купола Эти грани, однако, не располагаются в той же плоскости, что и исходные грани. Во-первых, новые вершины «проецируются наружу» на описанную сферу. На рис. 6.29, б показан процесс проецирования в сечении. Например, ребро между У, и У8 при разбиении образует две точки"images/tmp8E4A-385.png">
(А как задать И^,?) Проецирование 1У18 на описанную сферу радиуса Я является простым масшта бированием: где wl8 - радиус-вектор, связанный с точкой wis. Старые и новые вершины соединяются между собой отрезками прямых и образуют девять треугольных граней на каждую грань икосаэдра. (Почему геодезический купол не является новым Платоновым телом?) Чему равны значения е, f, v для этого полиэдра? Намного больше сведений о геодезических куполах можно найти в работах [Fuller, 72] и [Kappraff, 121].
Практические упражнения
