2 2

и (6.5)

W = lzlC+l-±+D. 2 2

Исходя из этого уравнения, нетрудно построить списки вершин и граней для усеченного куба (см. упражнения в конце раздела, а также тематическое задание 6.10).

www.nebopitera.ru прыжок с парашютом тандем цена спб.

Требование того, что все грани должны быть правильными полигонами и окружать каждую вершину в одном и том же порядке, ограничивает число полуправильных многогранников до 13 возможных1. Они будут рассмотрены позднее, в тематическом задании 6.10. Архимедовы тела все еще обладают достаточной симметрией, так что нормальный вектор к каждой грани может быть найден с использованием координат середины этой грани.

На рис. 6.26 изображено одно из Архимедовых тел, представляющее особый интерес: оно является усеченным икосаэдром 5 б2 и состоит из правильных гексагонов и пентагонов. Этот многогранник известен во всем мире, так как именно такую форму имеет футбольный мяч. В последнее время усеченный икосаэдр получил новое название - бакибол (buckyball) - в честь Бакминстера Фуллера (Buckminster Fuller) - из-за его интереса к подобным геодезическим структурам. Недавно кристаллографы обнаружили, что 60 атомов углерода могут располагаться в вершинах усеченного икосаэдра, образуя новый вид молекулы углерода, отличный от графита и алмаза. Этот материал обладает многими

1 Четырнадцатый полуправильный многогранник (псевдоромбокубооктаэдр) был открыт в 1957 году советским математиком В. Г. Ашкинузе, хотя западные ученые чаще приписывают это открытие югославскому математику С. Билинскому (публикация 1960 года). Псевдоромбокубооктаэдр получается из ромбокубооктаэдра поворотом «крышек» на 45° вокруг оси симметрии всего тела. - Поймем, пер.

6.3. Многогранники_._373

замечательными свойствами, например, устойчивостью к высоким температурам и сверхпроводимостью [Browne, 36]; неудивительно, что он получил имя фуллерин (fullerene).

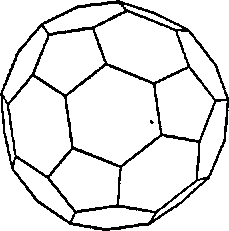
Рис. 6.26. Бакибол Весьма интересно моделировать бакибол и отображать его на графическом дисплее. Чтобы построить для него списки вершин и граней, нарисуем модель икосаэдра, изображенного на рис. 6.27, после чего разделим каждое ребро на три равные части. Вследствие этого на каждом ребре появятся две новые вершины, координаты которых могут быть легко вычислены. Пронумеруем 60 новых вершин, сообразуясь со своим вкусом, чтобы построить для бакибола список вершин. На рис. 6.27 приведена часть развертки икосаэдра с новыми вершинами, соединенными ребрами. Отметим, что каждая старая грань икосаэдра становится шестиугольником, а каждая старая вершина икосаэдра «срезается» и превращается в пятиугольную грань. Построение списка граней сводится к простому перечислению их согласно модели. В тематическом задании 6.10 проводится дальнейшее исследование Архимедовых тел.

⇐ Предыдущая| |Следующая ⇒