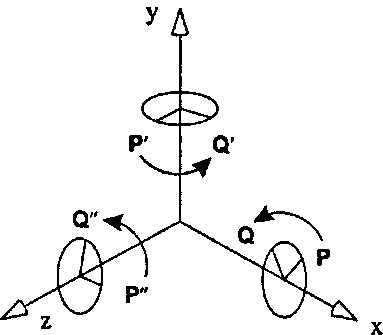
Рис. 5.25. Положительные повороты относительно трех координатных осей

(5.27)1 В левосторонней системе координат поворот на положительный угол (3 против часовой стрелки будет при взгляде наружу вдоль положительной осп из начала отсчета. Такая формулировка используется рядом авторов.
Преобразования объектов
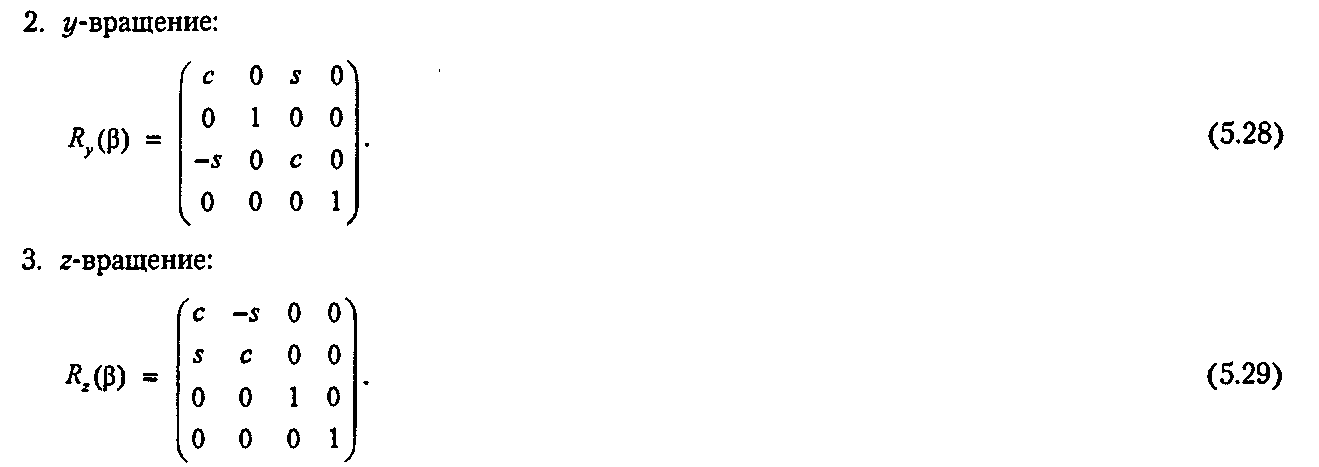
Отметим, что 12 элементов каждой матрицы являются нулями и единицами из единичной матрицы. Они находятся в последней строке и последнем столбце, а также в строке и столбце, соответствующих оси, вокруг которой производится вращение (например, для х-вращения это первая строка и первый столбец). Эти элементы гарантируют, что соответствующая координата преобразуемой точки не будет изменяться. Элементы с и 5 занимают оставшиеся места и всегда образуют вершины квадрата.
Отметим также, что элемент -« появляется в верхней строке квадрата для х-вращения и г-вращения, но в нижней строке квадрата для у-вращения. Имеет ли у-вращение какое-то существенное отличие? Этот вопрос исследуется в упражнениях.
Пример 5.3.1. Повороты сарая На рис. 5.26 нарисован «сарай» в его исходной ориентации (а), а также после х-вращения на -70° (б), у-вращения на 30° (в) и г-вращения на -90° (г).
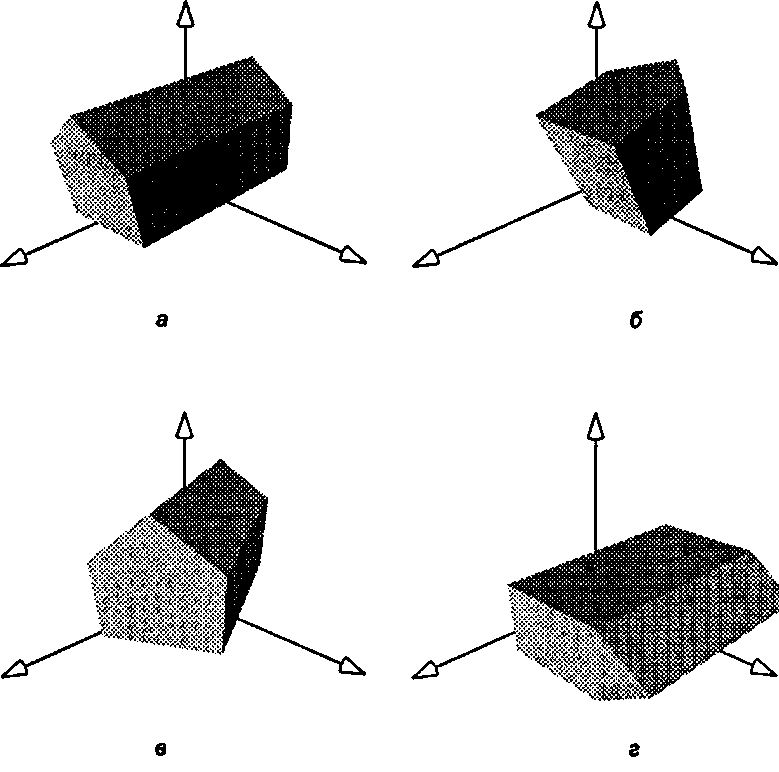
Рис. 5.26. Повороты базового сарая: а) сарай; б) х-вращение на -70°; в) у-вращение на 30°; г) г-вращение на 90°
5.3. Трехмерные аффинные преобразования
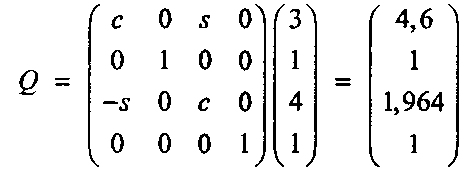
Пример 5.3.2
Поверните точку Р = (3,1,4) на 30° вокруг оси у. Решение Используя уравнение (5.28) при значениях с ш 0,866 и 5 ш 0,5, преобразуем точку Р в Как и ожидалось, координата у этой точки не изменилась.
Практические упражнения
5.3.1. Наглядное представление поворотов на 90° Нарисуйте правостороннюю трехмерную систему координат и убедитесь в том, что поворот на 90° (против часовой стрелки, если смотреть в сторону начала координат) вокруг каждой оси помещает каждую из оставшихся осей на место другой. Каков будет эффект от вращения точки на оси х вокруг самой оси х?
5.3.2. Поворот стандартного сарая
