Применение этого преобразования к точке (1,2) дает в результате (1,098,3,634). Этот результат является правильным, что может быть проверено путем вычерчивания на миллиметровке. (Проделайте это!)
Пример 5.2.6. Масштабирование и сдвиг относительно произвольных «опорных точек» Подобно тому, как это было сделано в примере 5.2.5, часто бывает необходимо масштабировать все точки относительно некоторой опорной точки, отличной от начала отсчета. Поскольку элементарная операция масштабирования из равенства (5.7) производит масштабирование относительно начала отсчета, нужно проделать ту же последовательность операций «перемещение - преобразование - обратное перемещение», что мы проделывали для поворотов. Такое масштабирование и обобщение операции сдвига рассматриваются в упражнениях в конце данного раздела.
Пример 5.2.7. Отражения относительно наклонной прямой Рассмотрим прямую линию, проходящую через начало отсчета и составляющую с осью х угол Р, как показано на рис. 5.18. Точка А отражается в точку В, а каждый из показанных на рисунке домиков отражается в другой домик. Мы хотим создать преобразование, которое отражает любую точку Р относительно прямой, называемой осью отражения (axis of reflection), в данную точку Q. Является ли это преобразование аффинным?
Чтобы показать, что это аффинное преобразование, построим его из трех частей: О поворот на угол Р (так, чтобы ось отражения совпала с осью х); О отражение относительно оси х, О обратный поворот на угол Р, «восстанавливающий» ось отражения.
5.2. Введение в преобразования
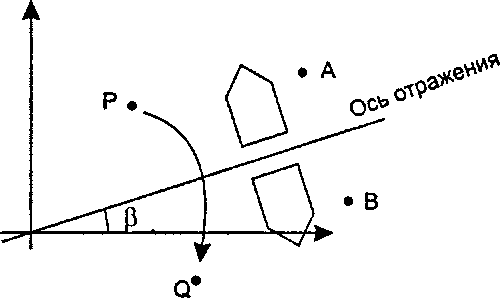
Рис. 5.18. Отражение точки относительно наклонной оси Каждое из этих преобразований представлено матрицей, и суммарное преобразование получается посредством умножения трех матриц, откуда следует, что суммарное преобразование является аффинным. Убедитесь в том, что каждый из этих этапов правильно представлен тремя приведенными ниже матрицами и что их произведение вычислено верно"images/tmp8E4A-280.png">
Здесь буквой с обозначено соз(-З), а буквой л - б1п (-(3). Используя тригонометрические тождества, напишем окончательный вид матрицы (проверьте это!):
