До сих пор все рассмотренные нами повороты были относительно начала отсчета. Но предположим, что вместо этого мы хотим поворачивать точки относительно какой-либо другой точки на плоскости. Как предложено на рис. 5.17, наша «опорная» точка - это точка V-(VX, Vy), и мы хотим повернуть точку Р на угол 0 до совпадения ее с точкой Q. Чтобы проделать это, нам нужно свести поворот относительно точки V к известному повороту относительно начала отсчета.
На рисунке показано, что если мы вначале преобразуем все точки так, чтобы точка V совпала с началом отсчета, то затем можно будет применить поворот относительно начала отсчета (преобразующий точку Р' в точку (У). После завершения этого поворота вся плоскость перемещается обратно, чтобы установить точку Vb прежнее положение. Таким образом, поворот состоит из следующих трех элементарных преобразований:
1. Переместить точку Р посредством вектора v - (~Vx, - V).
2. Повернуть относительно начала отсчета на угол 0.
3. Переместить точку Р обратно посредством вектора v.
Преобразования объектов
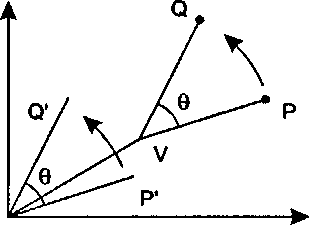
Рис. 5.17. Поворот относительно точки Создание матрицы для каждого элементарного преобразования и умножение этих матриц приводит к следующему"images/tmp8E4A-278.png">
где компоненты суммарного преобразования равны:
d- -Cos(Q)Vx + sin(0)V + Vx, dy=-sm(Q)Vx-cos(Q)Vy+Vx.Поскольку в полученном результате фигурируют те же самые члены cos(0) и sin(0), что и при повороте относительно начала отсчета, мы видим, что поворот относительно произвольной точки эквивалентен повороту относительно начала отсчета, за которым следует сложное перемещение с помощью (dx, dy).
В качестве характерного примера найдем преобразование, которое поворачивает точки на 30° относительно точки (-2, 3), и определим, в какую точку преобразуется точка (1, 2). При повороте на 30° используются величины cos(0) = 0,866 и sin(0) = 0,5. В этом случае вектор перемещения равен (1,232, 1,402), тогда преобразование, которое нужно применить к произвольной точке (Рх, Ру), равно:
Qx-0,866Px-0,5i>,+ 1,232, Q,-0,5Px+0,866i>,+ 1,402.