IV-МР, (5.16)
где суммарное преобразование представлено одной матрицей М-М3МҐ
(5.17)5.2. Введение в преобразования При использовании однородных координат аффинные преобразования компонуются посредством простого умножения матриц. Отметим, что матрицы расположены в порядке, обратном по отношению к тому, в котором эти преобразования применяются. Если мы сначала применяем преобразование Г, с матрицей М,, а затем к результату применяем преобразование Т2 с матрицей М2, то матрица суммарного преобразования равна М2М(, то есть вторая матрица в произведении стоит первой, если читать слева направо. (При преобразовании систем координат мы увидим как раз противоположный порядок.)
Рассуждая аналогично, любое количество аффинных преобразований может быть скомпоновано простым умножением соответствующих им матриц. Таким образом могут быть сформированы и заключены в одну матрицу преобразования, содержащие любую последовательность поворотов, масштабирований, сдвигов и переносов.
Приложение для накрутки лайков вконтакте приложение в вк. Лучший сервис по накрутке лайков в вк.
Пример 5.2.4. Построение композиции Постройте преобразование, которое: а) поворачивает на 45°, б) затем масштабирует вдоль х на 1,5 и вдоль у на -2, в) и, наконец, перемещает на вектор (3, 5). Решение Постройте три матрицы и перемножьте их в нужном порядке (первая идет последней и т. д.):
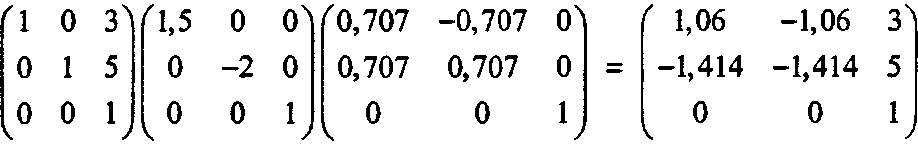
Теперь, чтобы преобразовать точку (1,2), расширим ее до тройки (1,2,1), затем умножим ее на композитную матрицу и в результате получим тройку (1,94,0,758,1). Затем отбросим 1, чтобы увидеть отображенную точку (1,94, 0,758). Полезно на миллиметровке произвести все эти преобразования поочередно, чтобы увидеть, как отображается исходная точка (1,2).
5.2.6. Примеры композиции двумерных преобразований Искусство - это задание схемы переживания, и наше эстетическое наслаждение заключается в принятии этой схемы.
Алфред Норт Уайтхед (Alfred North Whitehead)
В данном разделе мы разберем несколько важных примеров компоновки двумерных преобразований и посмотрим, как они себя ведут.
Пример 5.2.5. Поворот относительно произвольной точки