)Практические упражнения
5.2.5. Что является обратным преобразованием для поворота?
Докажите, что обратным преобразованием для поворота на угол 0 является поворот на угол -6. Обоснованно ли это геометрически? Почему?
5.2.6. Обращение сдвига Является ли обращение сдвига тоже сдвигом? Докажите, почему да или почему нет.
' Обзор обратных матриц дается в приложении 2.
Преобразования объектов
5.2.7. Обратная матрица Вычислите матрицу, обратную к данной:
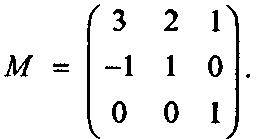
5.2.5. Композиция аффинных преобразований Прогресс - это неплохо - один раз, но он продолжается слишком долго.
Огден Нэш( Ogden Nash)
Не так уж часто мы выполняем только одно элементарное преобразование; обычно в приложении требуется, чтобы мы создали сложное преобразование из нескольких элементарных. Например, нам может понадобиться: О переместить на вектор (3, -4), О затем повернуть на 30°, О затем масштабировать с помощью множителя (2, -1), О затем переместить на (0, 1,5), О и, наконец, повернуть на -30°.
Как эти отдельные преобразования объединяются в одно суммарное преобразование? Процесс последовательного применения нескольких преобразований с целью формирования единого суммарного преобразования называется компоновкой, или композицией (composing), этих преобразований; иногда употребляется еще более сложный термин: конкатенация (concatenating). Как мы увидим, при компоновке двух аффинных преобразований результирующее преобразование является (к счастью) тоже аффинным.
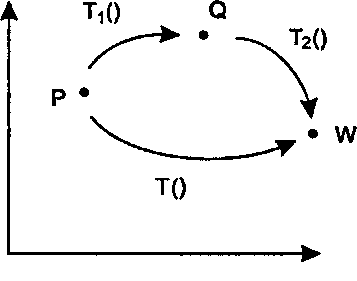
Рис. 5.16. Композиция двух преобразований Посмотрим, что происходит, когда компонуются два двумерных преобразования, Т{( ) и Т2( ). Как показано на рис. 5.16, Г,( ) преобразует точку Р в точку О, а Г2( ) преобразует точку (I в точку №. Какое преобразование Т( ) преобразует точку Р сразу в точку V/? Иными словами, какова сущность Ы-Т^-Т^Р))-}
Пусть эти два преобразования представлены матрицами М, и М2. Тогда точка Р вначале преобразуется в точку М,Р, которая затем преобразуется в М2(М,Р). В силу свойства ассоциативности последнее выражение равно (М2М,)Р, тогда мы имеем"opengl1_307.html">⇐ Предыдущая| |Следующая ⇒