На рис. 4.38 показаны двумерный полигон и трехмерный полиэдр, которые нам, возможно, нужно будет анализировать или визуализировать в графическом приложении. В связи с такими объектами возникают три следующих важных вопроса.
О Находится ли данная точка Р внутри или вне объекта?
О В каком месте данный луч Л первый раз пересечет объект?
О Какая часть данной прямой Ь лежит внутри объекта, а какая - вне его?
4.8. Задачи о пересечениях многоугольников Вот простой пример: какая часть (или части) прямой Зу - 2х - 6 лежит внутри полигона с вершинами (0,3), (-2, -2), (-5,0), (0, -7), (1,1)?
4.8.1. Работа с выпуклыми полигонами и полиэдрами Общий случай пересечения прямой с произвольным полигоном или полиэдром достаточно сложен, поэтому оставим его до раздела «Отсечение границами произвольных полигонов». Задача становится намного проще, когда полигон или полиэдр являются выпуклым, поскольку выпуклый полигон полностью описывается набором «ограничивающих прямых»; в трехмерном случае выпуклый полиэдр полностью описывается набором «ограничивающих плоскостей». Поэтому нам необходимо только проверить эту прямую на предмет пересечения с совокупностью неограниченных прямых или плоскостей.
Рисунок 4.39 иллюстрирует двумерный случай. На рис. 4.39, а показан выпуклый Пентагон (пятиугольник), на рис. 4.39, б - прямые Ьа, I, и т. д., ограничивающие этот Пентагон. Каждая ограничивающая прямая определяет два полупространства: внутреннее полупространство, которое содержит данный полигон, и внешнее полупространство, не имеющее с полигоном общих точек. Рисунок 4.39, в показывает часть внешнего полупространства, соответствующую ограничивающей прямой 12.
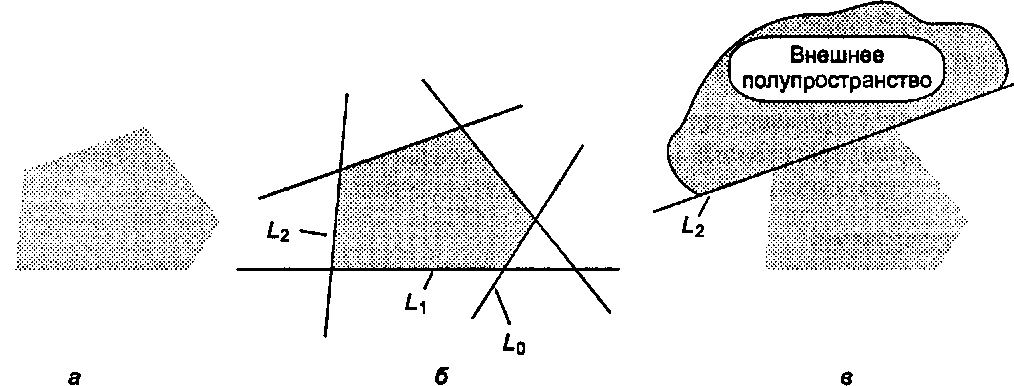
Рис. 4.39. Выпуклые полигоны и полиэдры
Пример 4.8.1. Определение ограничивающих прямых
На рис. 4.40, а показан единичный квадрат; четыре ограничивающих его прямых описываются уравнениями х = 1, х = -1, у = 1, у - -1. Кроме того, для каждой ограничивающей прямой мы можем указать внешний нормальный вектор, который направлен во внешнее полупространство, соответствующее данной ограничивающей прямой. Внешней нормалью для прямой у = 1 является, конечно, п = (0,1). (Чему равны остальные три внешние нормальные вектора?)
