2. а = (2, -4,3), с = (4,0, -4), п - (6,9,9), В - (-7,2,7).
3. а = (2,0), с = (0, -4), п - (0,8), в - (7,0).
4. а = (2,4, 3), с = (4,4, -4), п = (6,4,8), в - (7,4, 7).
1 Если же числитель также равен пулю, то луч целиком лежит в рассматриваемой прямой (для двумерного случая) или плоскости (в трехмерном случае). Почему?
Векторные инструменты для графики
'4.7.2. Соударение луча с плоскостью
Найдите точку, в которой луч (1,5,2) + (5, -2,6)г соударяется с плоскостью 2х - 4у + г = 8.
4.7.3. Чем является пересечение двух плоскостей?
Из геометрии мы знаем, что две плоскости пересекаются по прямой линии. Однако что это за прямая? Рассмотрим две плоскости, заданные уравнениями п (Р - А) = 0 и m (Р - В) = 0. Найдите параметрическую форму прямой, по которой они пересекаются. Возможно, наиболее простой вам покажется такая процедура.
1. Сначала запишите в параметрической форме одну из плоскостей, например вторую плоскость: В + as + Ьг.
2. Затем подставьте это выражение в точечную нормальную форму для первой плоскости и таким образом получите уравнение, связывающее параметры s и t.
3. Выразите из этого равенства s как функцию от г, например, s = E + Ft. (Найдите выражения для Е и F.)
4. Запишите искомую прямую в виде В + а(Е + Ft) + Ьг.
4.8. Задачи о пересечениях многоугольников Многоугольники (полигоны) являются основными объектами, используемыми как в двумерной, так и в трехмерной графике. В случае двумерной графики описывать и рисовать полигоны просто, так как они имеют прямые ребра. В трехмерной графике объект часто моделируется в виде «сетки» из полигонов - множества примыкающих друг к другу многоугольников, образующих «оболочку» («skin») объекта. Если эта оболочка образует замкнутую поверхность, ограничивающую некоторую часть пространства, то такая сетка называется многогранником, или полиэдром {polyhedron). Мы будем подробно изучать сетки и полиэдры в главе 6.
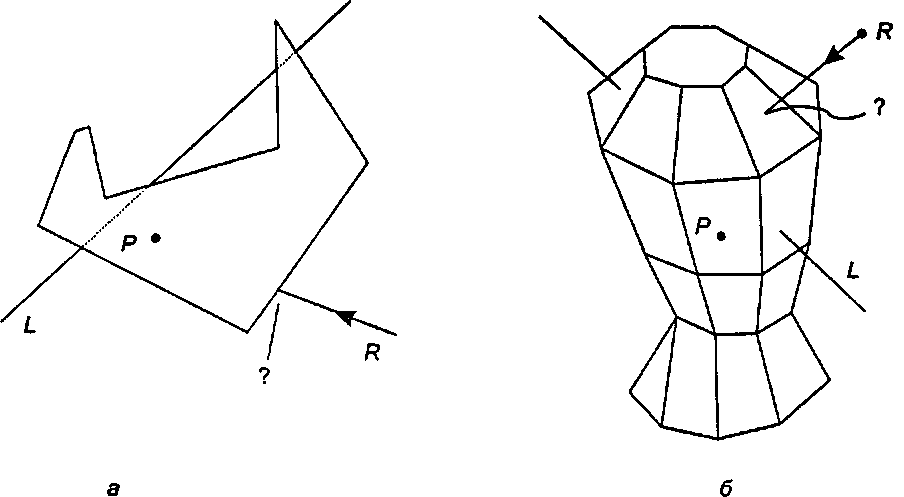
Рис. 4.38. Задачи пересечения прямой с полигональными объектами
