п(Л + с*Ьй-В)-0.
4.7. Пересечения прямых с плоскостями; отсечение Данное уравнение может быть переписано в следующем виде: п(А-В) + п-<аш-0, которое является линейным относительно гЫг Вот его решение: г = -^1 (время соударения, для двух и трех измерений). (4.59)
ПС
Как всегда в случаях с дробями, следует иметь в виду возможность обращения знаменателя формулы для ?Ы( в нуль. Такой случай имеет место при п с - 0, то есть когда луч параллелен плоскости, и тогда соударения нет вообще1.
Когда время соударения вычислено, легко определить положение точки соударения - просто подставим ?Ы1 в формулу для луча и получим: Р., = а + с£ы (точка соударения, случаи двух и трех измерений). (4.60)
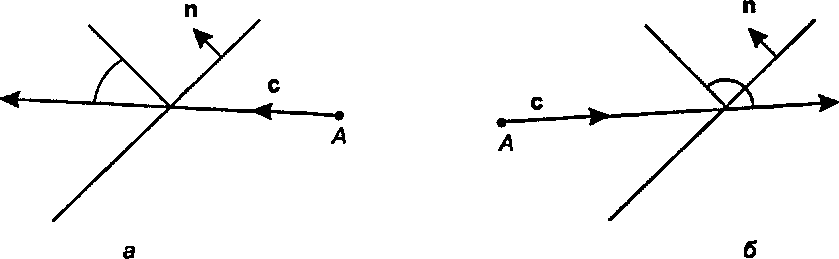
Рис. 4.37. Луч: а) сонаправленный с нормалью п и б) противоположно направленный к ней В практических упражнениях в конце этого раздела нам также нужно будет определить, в каком направлении луч падает на прямую или плоскость: «(направленно с нормалью п или противоположно направленно. (Эта ориентация будет важна по той причине, что нам понадобится знать, уходит луч от объекта или входит в него.) На рис. 4.37 показаны два возможных случая соударения луча с прямой. На рис. 4.37, а угол между направлением с луча и нормалью п меньше 90°, поэтому мы говорим, что луч сонаправлен с п. На рис. 4.37, б угол превышает 90°, поэтому луч противоположно направлен с нормалью п.
Легко проверить, какая из этих возможностей имеет место, поскольку знак скалярного произведения п с сразу говорит о том, меньше или больше 90° угол между п и с. Сведя воедино все сказанное выше, имеем три следующие возможности: если п с > 0, то луч сонаправлен с нормалью; если п с = 0, то луч параллелен прямой; (4.61) если п с < 0, то луч противоположно направлен с нормалью.
Практические упражнения
4.7.1. Пересечение луча с прямыми и плоскостями Найдите, где и когда луч а + сг соударяется с объектом п(Р -В)"0(с прямой для двух измерений, с плоскостью для трех измерений):
1. а = (2, 3), с = (4, -4), п - (6,8), в - (7, 7).
