В данном разделе мы рассмотрим другой метод, который годится как для прямых, так и для плоскостей. В нем пересекающая прямая представляется параметрически, а пересекаемая прямая или плоскость - в точечной нормальной форме. Этот метод является непосредственным и в нем ясно видна суть происходящего. Мы разработаем его один раз, а затем применим его результаты к задаче отсечения прямой линии границами выпуклого двумерного многоугольника или выпуклого трехмерного многогранника. В главе 7 мы увидим, что такая техника пересечения является важнейшим этапом при отображении трехмерных объектов. В главе 14 мы используем ту же технику пересечения при выполнении трассировки лучей.

моторное масло равенол оптом ростов. гузмания микс как быстро растут.

Если в двумерном пространстве мы находили точку пересечения прямой с другой прямой, в трехмерном пространстве обычно нам необходимо найти точку пересечения прямой с плоскостью. Обе эти задачи можно решить за один прием, поскольку задача формулируется в терминах скалярных произведений, вследствие чего одни и те же выражения описывают двумерные и трехмерные векторы. (Задача о пересечении двух плоскостей будет рассматриваться в упражнениях в конце главы; ее решение также основано на скалярном произведении.)

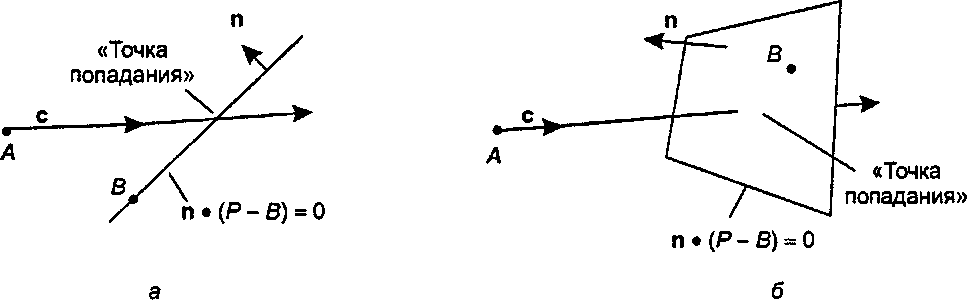
Рис. 4.36. Где луч пересекает прямую или плоскость?

Рассмотрим прямую, которая параметрически описывается формулой R(t) = A + ct. Будем называть ее также лучом (ray). Мы хотим определить, где этот луч пересекает объект, заданный в точечной нормальной форме п(Р - В) = 0. В двумерном пространстве этот объект является прямой линией, а в трехмерном - плоскостью. В любом случае точка В расположена на этом объекте, а вектор п - нормален к нему. На рис. 4.36, а показан луч, падающий на прямую, а на рис. 4.36, б - на плоскость. Мы хотим найти положение «точки соударения».

Допустим, что соударение происходит при г = ?hit, в «момент соударения». При этом значении г прямая и луч должны иметь одинаковые координаты, поэтому А + cthit должно удовлетворять уравнению точечной нормальной формы для прямой или плоскости. Подставим эту неизвестную «точку соударения» в точечное нормальное уравнение и получим следующее условие для £hit"opengl1_266.html">⇐ Предыдущая| |Следующая ⇒