Практические упражнения Б3.1. Операция деления Покажите, что если г и т - комплексные числа, то Л - Н е'(Ац(0-А-вМ) _ 2ХЮ* _ 2ХЮ*
т тютю* |да|2
Б3.2. Отношение, модуль которого всегда равен единице Покажите, что модуль отношения двух комплексно-сопряженных чисел (а + гЬ)/(а - г'6) для любых а и Ъ равен единице.
БЗ.З. В каком случае четыре комплексных числа лежат на одной окружности?
Покажите, что А^((г3 - г1)/(г2 - г,)) - А^((г4 - 2,)/(г4 - г2)) тогда и только тогда, когда г,,…, г4 лежат на одной окружности, а на прямой линии тогда и только тогда, когда отношение [(г3 - 2^/{г2 - г^]/ [(г4 - 2г)/(24 ~ 22)] вещественно.
Б4. Сферические координаты и направляющие косинусы
В данном разделе излагается понятие сферических координат, а также преобразование из сферических координат в декартовы и обратно.
На рис. Б.З показано, как определяется точка U в сферических координатах. Расстояние от точки U от начала координат равно R, а ф означает угол, образуемый радиус-вектором точки U с плоскостью xz; этот угол носит название широты (latitude) точки U. Угол 9 называется долготой, или азимутом (azimuth), точки U, это угол между плоскостью ху и плоскостью, проходящей через точку U и ось у. Угол ф лежит в интервале -л/2 <ф< л/2, а угол 9 - в интервале 0 < 9 < 2л.
При помощи простых тригонометрических преобразований можно вывести соотношения между этими величинами и декартовыми координатами точки U(ux, иу, иг). Эти соотношения имеют следующий вид: их - /?cos(0) cos(9),
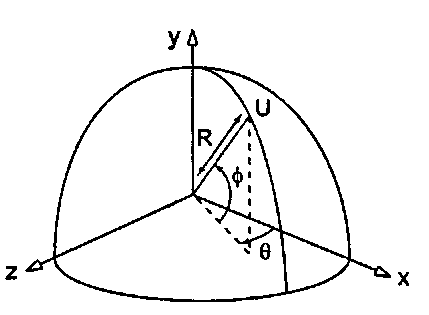
Рис. Б.З. Сферические координаты
Uy = J?sin(0),иг - i?sin(0) sin(9).
(Б.4)
Приложение Б. Немного математики для компьютерной графики Можно обратить эти соотношения и выразить (R, ф, 9) через (и , и , и )"images/tmp8E4A-987.png">
(Б.5)
Приведенная здесь функция ап^(,) является двухаргументной формой арктангенса и определяется так:
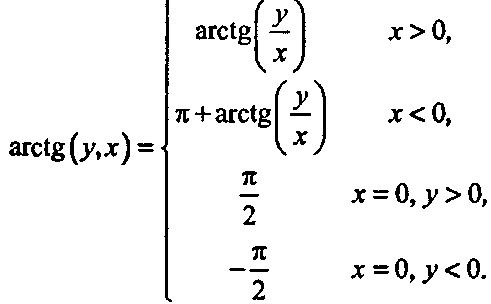
(Б.6)
Эта функция может отличать случай, когда х и у положительны, от случая, когда они оба отрицательны, в отличие от обычной функции arctg(t//*), которая всегда выдает углы в диапазоне от -л/2 до л/2.
Пример Б4.1
